Основы ядерной физики и радиоактивности

Состав ядра

Атом имеет планетарную модель: положительно заряженное ядро и электроны вокруг него.
Ядро состоит из:

Протонов (заряд $ +e $, масса ≈ масса нейтрона, число протонов = Z – зарядовое число);
Нейтронов (без заряда, масса ≈ масса протона).

Общее число нуклонов называют массовым числом A:
$$
A = Z + N
$$

Атомы с одинаковым $ Z $, но разным $ N $ называются изотопами.

Обозначение ядер:
$$
^A_Z X
$$
(например, $ ^4_2He $).

Основная единица – электронвольт (эВ):
$$
1 \text{ эВ} = 1.6 \cdot 10^{-19} , Дж
$$

Используются приставки: кэВ, МэВ.

Ядерные силы и энергия связи

Ядерные силы удерживают нуклоны, противодействуя кулоновскому отталкиванию.

Особенности:

действуют на расстояниях < $ 10^{-15} , м $;
сильнее электромагнитных;
не зависят от заряда;
обладают насыщением.

Энергия связи ядра:
$$
E_{св} = \Delta m , c^2 = (Z m_p + N m_n - m_{я})c^2
$$

где $ \Delta m $ – дефект масс.

Удельная энергия связи:
$$
E_{уд} = \frac{E_{св}}{A}
$$

Радиоактивность – самопроизвольный распад ядер с испусканием частиц.

Закон радиоактивного распада:
$$
N(t) = N_0 \cdot 2^{-t/T}
$$
где $ T $ – период полураспада.

Виды распада:

Альфа-распад:
$$
^A_ZX \to ^{A-4}_{Z-2}Y + ^4_2He
$$
Бета-распад:
$$
^A_ZX \to ^A_{Z+1}Y + e^- + \tilde{\nu}_e
$$

Ядерная реакция — превращение ядер при взаимодействии с частицами.

Пример:
$$ ^7_3Li + ^1_1p \to 2 \, ^4_2He $$
Законы:

Сохраняется массовое число и заряд.
Дефект масс превращается в энергию: $$ E = \Delta m \, c^2 $$

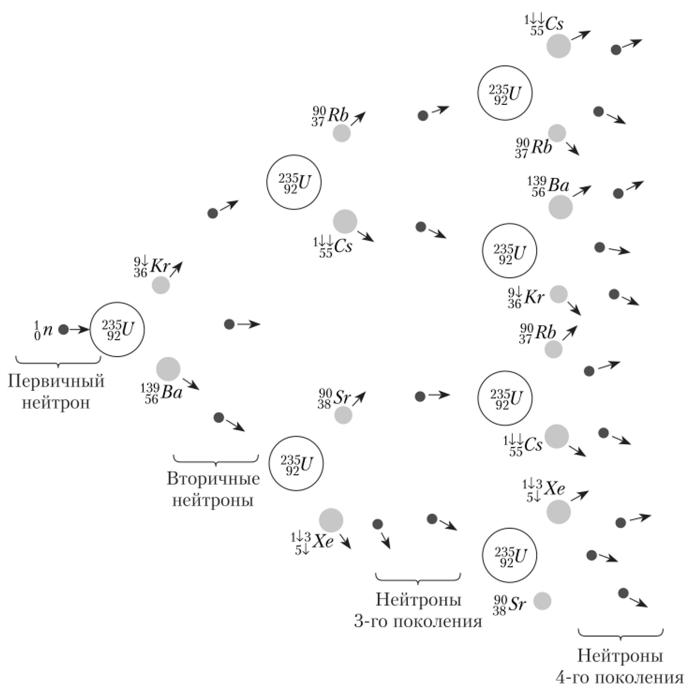
Деление тяжёлых ядер и цепные реакции

При захвате нейтрона тяжёлое ядро (например, уран-235 или плутоний-239) становится нестабильным и распадается на два более лёгких ядра, при этом выделяется большое количество энергии.
В процессе также испускается несколько нейтронов, которые могут вызывать дальнейшие деления и поддерживать цепную реакцию.

Условия цепной реакции:

наличие критической массы;
подходящая скорость нейтронов;
отсутствие примесей-поглотителей нейтронов.
корости нейтронов, отсутствие примесей-поглотителей.

Детекторы излучений

Ионизационные камеры, счётчик Гейгера
Камера Вильсона, пузырьковая камера
Сцинтилляционный счётчик, ядерная эмульсия

Кратко: выбор детектора зависит от типа и энергии излучения и условий измерения.

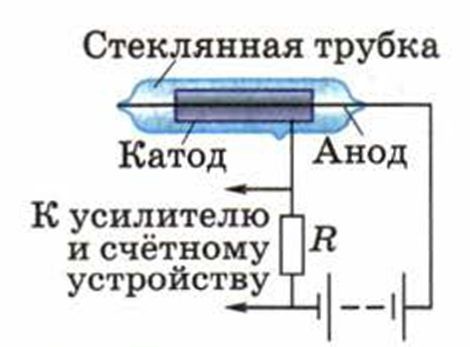
Приборы для регистрации излучения

Примеры решение задач:

1.Сколько энергии выделится, если тело массой 15 г полностью превратить в энергию?
Сколько фотонов с частотой $ 3 \cdot 10^{15} , Гц $ можно при этом получить?

$ Дано:$
$ m = 15 \, г = 0.015 \, кг $
$ \nu = 3 \cdot 10^{15} \, Гц $
$ c = 3 \cdot 10^8 \, м/с $
$ h = 6.626 \cdot 10^{-34} \, Дж \cdot c $
$ Найти: E, \, N $

$ Решение:$
Используем формулу эквивалентности массы и энергии:
$$ E = mc^2 = 0.015 \cdot (3 \cdot 10^8)^2 = 1.35 \cdot 10^{15} \, Дж $$ Энергия одного фотона:
$$ \varepsilon = h\nu = 6.626 \cdot 10^{-34} \cdot 3 \cdot 10^{15} \approx 1.99 \cdot 10^{-18} \, Дж $$ Число фотонов:
$$ N = \frac{E}{\varepsilon} = \frac{1.35 \cdot 10^{15}}{1.99 \cdot 10^{-18}} \approx 6.8 \cdot 10^{32} $$
$ Ответ: E = 1.35 \cdot 10^{15} \, Дж, \, N \approx 6.8 \cdot 10^{32} $

2.Рассчитайте энергию, выделяющуюся в реакции:
$ ^7_3Li + ^1_1H \to ^4_2He + ^4_2He $

Известно, что массы частиц:
$ m_{Li} = 7.01601 , а.е.м $,
$ m_{He} = 4.00260 , а.е.м $,
$ m_H = 1.00783 , а.е.м $.
$ 1 , а.е.м \cdot c^2 = 931.5 , МэВ $.

$ Дано:$
$ ^7_3Li + ^1_1H \to 2 \, ^4_2He $
$ m_{Li} = 7.01601 \, а.е.м $
$ m_H = 1.00783 \, а.е.м $
$ m_{He} = 4.00260 \, а.е.м $
$ 1 \, а.е.м \cdot c^2 = 931.5 \, МэВ $
$ Найти: E $

$ Решение:$
Масса до реакции:
$$ m_{\text{до}} = m_{Li} + m_H = 7.01601 + 1.00783 = 8.02384 \, а.е.м $$ Масса после реакции:
$$ m_{\text{после}} = 2 m_{He} = 2 \cdot 4.00260 = 8.00520 \, а.е.м $$ Дефект масс:
$$ \Delta m = m_{\text{до}} - m_{\text{после}} = 8.02384 - 8.00520 = 0.01864 \, а.е.м $$ Энергия реакции:
$$ E = \Delta m \cdot 931.5 \approx 17.4 \, МэВ $$
$ Ответ: E \approx 17.4 \, МэВ $

Задача №3.
Некоторое ядро подверглось 5-ти $\alpha$-распадам и неизвестному числу $\beta^-$-распадов.
После реакций осталось $ ^{209}_{84}Po $.
Определите элемент, с которого началась реакция. Рассчитайте число $\beta$-распадов.

$ Дано:$
После распадов осталось $ ^{209}_{84}Po $
Было 5 $\alpha$-распадов
Было $ n $ $\beta^-$-распадов
$ Найти:$ начальное ядро и $ n $

$ Решение:$
1. При $\alpha$-распаде: $ A \to A-4,\; Z \to Z-2 $.
После 5 $\alpha$-распадов:
$$ A_{\text{нач}} = 209 + 5\cdot4 = 229 $$ $$ Z_{\alpha} = 84 + 5\cdot2 = 94 $$
2. Каждый $\beta^-$-распад увеличивает $ Z $ на 1.
Пусть их было $ n $. Тогда:
$$ Z_{\text{нач}} = Z_{\alpha} - n $$ Подставим: $$ 84 = 94 - n \;\;\Rightarrow\;\; n = 10 $$
3. Следовательно:
$$ A_{\text{нач}} = 229,\; Z_{\text{нач}} = 84 $$ Это элемент Polonium ($Po$).

$ Ответ:$ начальное ядро — $ ^{229}_{84}Po $, число $\beta^-$-распадов $ n=10 $.