Поверхностное натяжение жидкости. Капиллярные явления.

Основные термины:

• сила молекулярного давления
• свободная поверхность жидкости
• сила поверхностного натяжения
• коэффициент поверхностного натяжения
• капилляры

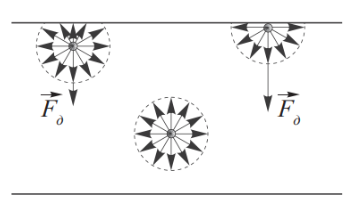
В отличие от газов, в жидкостях кинетическая энергия молекул примерно равна их потенциальной энергии. На каждую молекулу жидкости действуют силы притяжения со стороны молекул, находящихся на расстоянии порядка \(10^{-9}\ м\). Геометрическая сумма сил, действующих на молекулы в глубине жидкости, равна нулю. У молекул, находящихся на поверхности жидкости, сфера молекулярного взаимодействия частично заполнена молекулами воздуха, силами взаимодействия которых можно пренебречь. Равнодействующую сил взаимодействия молекул поверхностного слоя жидкости называют силой молекулярного давления.

Сила молекулярного давления – это результирующая сил, действующих на молекулы поверхностного слоя жидкости, направленная перпендикулярно ее свободной поверхности.
Сила молекулярного давления заставляет молекулы «втягиваться» внутрь жидкости. Поэтому жидкости при отсутствии на них сил (например, в невесомости) принимают форму шара. Это объясняется тем, что для такого объема жидкости поверхность шара минимальна. Жидкость принимает форму шара, так как в этом случае потенциальная энергия ее поверхностного слоя наименьшая.
Свободная поверхность жидкости стремится сократиться. Это можно наблюдать в том случае, когда жидкость принимает форму тонкой пленки. Это происходит, например, при выдувании мыльных пузырей. Свойство поверхности жидкости сокращаться, можно истолковать как существование сил, стремящихся сократить эту поверхность. Эти силы называют силами поверхностного натяжения.

Силы поверхностного натяжения – это силы взаимного притяжения молекул поверхностного слоя жидкости, направленные по касательной к поверхности и стремящиеся уменьшить ее площадь. $$\sigma = \frac{F}{l}$$ \( где\ \sigma - коэффициент\ поверхностного\ натяжения,\)
\(F - сила\ поверхностного\ натяжения,\)
\(l - длина\ границы\ свободной\ поверхности\ жидкости\)

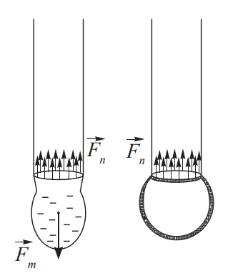
Для капли жидкости, отрывающейся от трубки малого диаметра, границей поверхностного слоя является длина окружности, радиус которой равен внутреннему радиусу трубки. $$l = 2 \pi R = \pi d$$ Капля отрывается в момент, когда вес капли становится равным силе натяжения: $$P = F_Н$$ $$\sigma = \frac{mg}{\pi d}$$ Коэффициент поверхностного натяжения зависит от рода жидкости, ее температуры и наличия в ней примесей. При повышении температуры и при наличии примесей коэффициент поверхностного натяжения уменьшается.

Капиллярные явления
Капля воды растекается по чистой поверхности стола, но не растекается по жирной поверхности, а имеет форму почти правильного шарика. В первом случае говорят, что вода смачивает поверхность, а во втором — не смачивает. В первом случае сила взаимодействия молекул жидкости друг другом меньше, чем сила взаимодействия с молекулами твердого тела. Под действие этих сил (а также под действием силы тяжести) жидкость растекается по поверхности стола.
Во втором случае наоборот: сила притяжения молекул жидкости друг с другом больше силы взаимодействия с молекулами твердого тела, и поэтому жидкость принимает шарообразную форму.
Взаимодействие жидкости со смачивающими и не смачивающими поверхностями твердых тел является причиной капиллярных явлений.

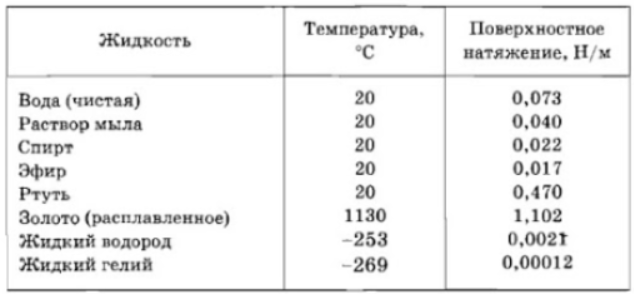
Капилляры – это трубки с очень малым внутренним диаметром. В переводе с латыни \(«капиллус»\ −\ «волос»\). Уровень жидкости в капиллярной трубке поднимается в сравнении с уровнем жидкости в сосуде, если она смачивает стенки трубки. Подъем жидкости происходит до тех пор, пока сила тяжести, действующая на столб жидкости в капилляре, не станет равной силе поверхностного натяжения: $$F_{Тяж} = F_{Нат}$$ $$F_{Тяж} = mg = \rho Shg = \rho \pi r^2 hg; \quad \quad \quad F_{Тяж} = \sigma l = \sigma \cdot 2\pi r$$ $$\rho \pi r^2 hg = \sigma \cdot 2\pi r \quad \quad \quad \quad \Rightarrow \quad \quad \quad \quad h = \frac{2 \sigma}{\rho gr}$$

Примеры решения задач:

1.Какую массу имеет капля воды, вытекающая из стеклянной трубки диаметром \(10^{-3}\ м\), если считать что диаметр шейки капли равен диаметру трубки?

2.В спирт опущена трубка. Диаметр ее внутреннего канала равен \(0,5\ мм.\) На какую высоту поднимется спирт в трубке? Плотность спирта \(800\ кг/м^3\)

3.Спичка длиной \(l = 4\ см\) плавает на поверхности воды. Если по одну сторону от спички налить касторовое масло, то она придет в движение. Определите силу, действующую на спичку, и ее направление. Коэффициенты поверхностного масла и воды \(\sigma_1 = 33\ мН/м\) и \(\sigma_2 = 72\ мН/м\) соответственно.

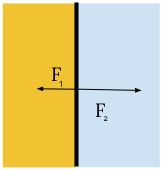
\(Дано:\) \(l = 4\ см = 4 \cdot 10^{-2}\ м\) \(\sigma_1 = 33\ мН/м = 33 \cdot 10^{-3}\ Н/м\) \(\sigma_2 = 72\ мН/м = 72 \cdot 10^{-3}\ Н/м\) \(Найти: F = ?\)		\(Решение:\) Предположим что касторовое масло находится слева от спички. На спичку действует одновременно две силы с двух разных сторон. Справа налево сила натяжения касторового масла и слева направо сила натяжения воды. Наша задача, найти равнодействующую силу и ее направление. $$\vec{F} = \vec{F_1} + \vec{F_2}$$ С учетом направлений сил, результирующая сила будет равна разности сил: $$F = | F_1 - F_2 |$$
	Сила поверхностного натяжения находится по формуле \(F = \sigma l\) Сила со стороны касторового масла: $$F_1 = \sigma_1 \cdot l = 33 \cdot 10^{-3} \cdot 4 \cdot 10^{-2} = 132 \cdot 10^{-5}\ Н$$ Сила со стороны воды: $$F_2 = \sigma_2 \cdot l = 72 \cdot 10^{-3} \cdot 4 \cdot 10^{-2} = 288 \cdot 10^{-5}\ Н$$ Сила со стороны воды больше, поэтому равнодействующая сила будет направлена в ту же сторону что и сила натяжения со стороны воды, направо. А его значение будет: $$F = F_2 - F_1 = 288 \cdot 10^{-5} - 132 \cdot 10^{-5} = 156 \cdot 10^{-5}\ Н$$ \(Ответ: 156 \cdot 10^{-5}\ Н\)