Кристаллы. Аморфные тела. Механические свойства твердых тел. Механическое напряжение. Закон Гука

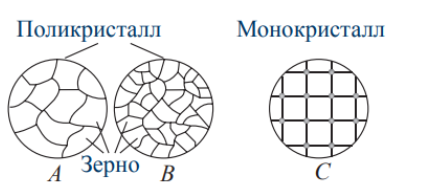
В физике все предметы делят на кристаллические и аморфные тела. Кристаллические тела могут быть монокристаллическими (состоят из одного кристалла) и поликристаллическими (состоят из многих кристаллов).

Свойства кристаллов:

• Имеют кристаллическую решетку. Кристаллическая решетка – это пространственное периодическое расположение атомов или ионов в кристалле. Точки кристаллической решетки, в которых расположены атомы или ионы, называются узлами кристаллической решетки. Все кристаллические решетки разделяют на четыре типа: ионные, атомные, молекулярные и металлические.
• Прочность и твердость. Способность тела противостоять разрушению под действием внешних сил называют прочностью. Твердость – это свойство материала разрушать поверхность других материалов.
• Анизотропность – это зависимость физических свойств (рост, прочность, деформация, теплопроводность) вещества от выбранного в них направления.
• Упругость - свойство материала восстанавливать свою форму.
• Определенная температура плавления и кристаллизации.
• Полиморфизм (углерод, алмаз, графит).
• Рост кристаллов (из растворов, расплавов, паров).

Свойства аморфных тел:

• Нет правильной формы (кристаллической формы).
• Изотропность – это независимость физических свойств вещества от выбранного в нем направления.
• Пластичность - свойство сохранять приобретенную под действием внешних сил форму.
• При кратком воздействии ведут себя как твердые тела, при длительном текут.

Деформацию сжатия и растяжения характеризуют абсолютным удлинением. Абсолютное удлинение \(\Delta l\) − величина, равная разности длин образца до деформации \(l_0\) , и после нее \(l\): $$\Delta l = l - l_0$$ При растяжении \(\Delta l\) − положительно, при сжатии − отрицательно.
Отношение абсолютного удлинения к длине тела до деформации \(l_0\) называют относительным удлинением: $$\varepsilon = \frac{\Delta l}{l_0}$$
При деформации тела в каждом его сечении в результате изменения расстояния между молекулами действуют электромагнитные силы, которые называют силами упругости или силами внутреннего напряжения. Распределение сил характеризует механическое напряжение.

Механическое напряжение \(\sigma\) – это физическая величина, равная силе внутреннего напряжения \(F_{упр}\), действующей на единицу площади поперечного сечения \(S\): $$\sigma = \frac{F_{упр}}{S}$$ Опытным путем английский физик Р. Гук пришел к следующему выводу:
Механическое напряжение упругого деформированного тела прямо пропорционально модулю упругости и относительному удлинению. $$\sigma = E \cdot \varepsilon$$ \(где\ E\ -\ Модуль\ Юнга\)
\(\varepsilon\ -\ относительное\ удлинение\)
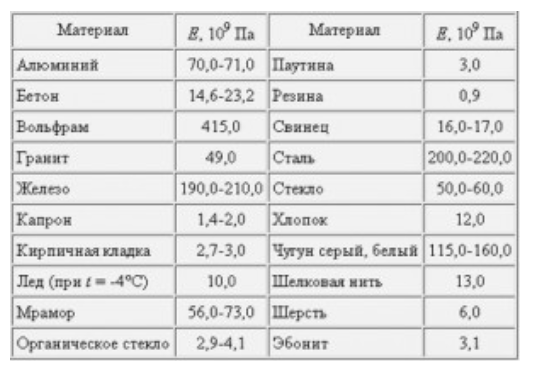
Мо́дуль Ю́нга — физическая величина, характеризующая способность материала сопротивляться растяжению, сжатию при упругой деформации. Измеряется в Паскалях [Па]. $$\frac{F_{упр}}{S} = E \cdot \varepsilon \quad \quad \quad \Rightarrow \quad \quad \quad \frac{F_{упр}}{S} = E \cdot \frac{\Delta l}{l_0} \quad \quad \quad \Rightarrow $$ $$F_{упр} = \frac{E \cdot |\Delta l |}{l_0} \cdot S = \frac{E \cdot S}{l_0} \cdot |\Delta l | = k\ |\Delta l|$$ $$k = \frac{E \cdot S}{l_0} $$ \(где\ k\ -\ коэффициент\ жесткости\ пружины\)
Коэффициент жесткости зависит от размеров тела и упругих свойств вещества. Чем короче тело и чем больше площадь его поперечного сечения, тем оно жестче.

Примеры решения задач:

1.Под действием какой силы, направленной вдоль оси стержня, в нем возникает напряжение \(150\ МПа\)? Диаметр стержня равен \(4\ мм\).

2.Какую растягивающую силу надо приложить к стальной проволоке длиной \(3,6\ м\) и площадью поперечного сечения \(10^{-6}\ м^2\) для удлинения ее на \(2\ мм\)?