- +7 701 537 76 67
Работа. Мощность. Энергия. Закон сохранения механической энергии
Основные термины:
- Работа
- Энергия
- Закон сохранения энергии
Работа \(А\) - скалярная физическая величина, численно равная произведению модуля силы на перемещение и на косинус угла между вектором силы и вектором перемещения:
$$A = \vec{F} \cdot \vec{S} \cdot \cos \alpha \quad \quad \quad [Дж]$$
Работа против силы тяжести. Если тело равномерно поднимается, т.е. Движется с постоянной скоростью в направлении противоположном направлению действия силы тяжести, то, согласно формуле \(A\ =\ FS\), над телом совершается работа, где сила \(F\) совпадает с перемещением и равна по величине \(mg\).
$$A\ =\ \vec{F} \cdot \vec{S} = mgh$$
Работа против сил трения. Если тело движется с постоянной скоростью (равномерно) против сил трения, то над ним совершается работа:
$$A = F_{тр} \cdot S = \mu NS$$
Работа, затрачиваемая на упругую деформацию тела. Если пружина растягивается на длину \(\Delta x\), то действующая на пружину сила в соответствии с выражением \(F\ =\ kx\) возрастает пропорционально (\Delta x) от \(0\) до \(F_{max}). То работа равна:
$$A = F_{ср} \cdot \Delta x = \frac{k \Delta x^2}{2}$$
Мощность N - это физическая величина определяющая работу совершенную за единицу времени:
$$ N = \frac{A}{t} \quad \quad \quad \quad [Вт]$$
Если на тело действует постоянная сила, то мощность равна: \(N = \frac{F S \cos \alpha}{t} = F v \cos \alpha\)
\( \alpha \ -\ угол\ между\ направлениями\ силы\ и\ скорости\ тела\)
Энергия.
Любая работа, совершаемая над телом, увеличивает его энергию и делает его способным в свою очередь совершать работу. Энергией \(E\) называется способность тела совершать работу. Энергия измеряется в тех же единицах что и работа.
Кинетическая энергия - энергия, которой обладают тела в движении. “Кинетикос” по гречески означает “относящийся к движению”. Если тело находится в состоянии покоя, кинетическая энергия тела равна нулю. Она напрямую зависит от массы \(m\) и скорости \(v\) тела.
$$E_k = \frac{mv^2}{2}$$
\(m\ -\ масса\ тела\ [кг]; \quad \quad v -\ скорость\ движения\ тела\ [м/с];\)
Потенциальная энергия - это энергия взаимодействия тел. Потенциальная энергия тела, поднятого на некоторую высоту над поверхностью Земли:
$$E_p = mgh$$
\(m\ -\ масса\ тела\ [кг];\quad \quad g\ -\ ускорение\ свободного\ падения\ [м/с^2];\quad \quad h\ -\ высота\ [м];\)
Если тело деформировать в пределах упругой деформации, тогда после снятия внешней действующей силы тело возвращается в первоначальное состояние и при этом может совершать работу. Потенциальная энергия упруго деформированного тела:
$$E_p = \frac{k \Delta x^2}{2}$$
Силу называют потенциальной (консервативной), если работа этой силы не зависит от формы траектории, а зависит только от начального и конечного положения.
Полная механическая энергия \(E\) - это сумма кинетической и потенциальной энергии тела (системы):
$$E\ =\ E_p\ +\ E_k$$
Закон сохранения полной механической энергии: если на тела системы действуют только консервативные силы (силы тяжести, упругости, электростатические), то полная механическая энергия с течением времени не изменяется:
$$E\ =\ E_p\ +\ E_k =\ const.$$
Энергия не исчезает и не возникает снова, она только превращается из одного вида энергии в другой вид энергии или переходит от одного тела к другому.
Физические системы, в которых сохраняется полная механическая энергия, называются консервативными.
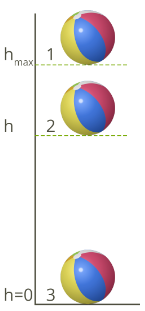
|
Посмотрим какие превращения энергии происходят при падении мяча массой \(m\) с некоторой высоты \(h_{max}\) на землю (без начальной скорости). В верхней точке траектории на высоте \(h_{max}\) (положение 1) мяч покоится , значит, его кинетическая энергия равна нулю (минимальна). \(E_{k\ min} = 0\) , а потенциальная энергия равна максимальному значению \(E_{p\ max}\ =\ mgh_{max}\) . Когда мяч начинает свое движение вниз, его высота относительно Земли уменьшается. Значит, уменьшается и потенциальная энергия. Скорость движения мяча при этом увеличивается, и растет кинетическая энергия. Таким образом, в любой точке своей траектории, кроме самой верхней и самой нижней точки (например, в положении 2), мяч обладает и потенциальной и кинетической энергией. $$E_k\ =\ \frac{mv^2}{2}, \quad E_p = mgh$$ С каждой секундой потенциальная энергия уменьшается, а кинетическая растет. Но их общая сумма остается постоянной. То есть, энергия превращается из одного вида (потенциальной) в другой вид (кинетическая). В самой нижней точке (в положении 3) тело уже находится на поверхности Земли и имеет потенциальную энергию равной нулю и максимальную кинетическую энергию. $$ E_{p\ min} = 0, \quad E_{k\ max} = \frac{mv^2}{2}$$ Получается что в этой точке потенциальная энергия полностью превратилось в кинетическую энергию. Но их максимальные значения равны между собой. $$E\ =\ E_{p\ max}\ +\ 0 = 0 + E_{k\ max} \quad \quad \Rightarrow \quad \quad E = E_{k\ max} = E_{p\ max}$$ |
Коэффициент полезного действия показывает насколько эффективно используется подводимая нему энергия. КПД (коэффициентом полезного действия) называют отношение полезной работы к полной работе.
\(A_{пол}\)– «полезная работа» – работа, которую необходимо выполнить;
\(A_{полн}\) – «полная работа» – работа, которую совершили;
\(\eta\) – коэффициент полезного действия (\(\eta\) – греческая буква, читается «эта»)
$$\eta = \frac{A_{пол}}{A_{полн}}$$
Коэффициент полезного действия выражается чаще не в долях от целого, а в процентах. Для этого отношение полезной работы к совершенной умножают на 100%
$$\eta = \frac{A_{пол}}{A_{полн}} \cdot 100 % $$
Примеры решения задач
1. Действуя силой \(80\ Н\), человек поднимает из колодца глубиной \(10\ м\) ведро воды за \(20\ с\). Какую мощность развивает при этом человек?
|
\(Дано:\)
\(F = 80\ Н\) \(h = 10\ м\) \(t = 20\ с\) \(Найти: N = ?\) |
\(Решение:\)
Формула для нахождения мощности выглядит следующим образом: \(A = N \cdot t \quad \Rightarrow \quad N = \frac{A}{t}\) Работа, совершенная в данном случае, найдется следующим образом: \(A = F \cdot h\) Тогда $$N = \frac{A}{t} = \frac{F \cdot h}{t} = \frac{80 \cdot 10}{20} = 40\ Вт$$ \(Ответ:\ N =\ 40\ Вт\) |
2. Мощность двигателя подъемного крана \(4\ кВт\). Груз какой массы он может поднять на высоту \(15\ м\) за \(2\ мин\).
|
\(Дано:\)
\(N = 4\ кВт\) \(h = 15\ м\) \(t = 2\ мин = 120\ с\) \(Найти: m = ?\) |
\(Решение:\)
Проделанная работа в зависимости от мощности находится следующим образом: \(A = N \cdot t\) Так как работа была совершена против силы тяжести, и тело переместилось на \(h\), то работа: \(A = m \cdot g \cdot h\) Тогда: $$m = \frac{A}{g \cdot h} = \frac{N \cdot t}{g \cdot h} = \frac{4000 \cdot 120}{10 \cdot 15} = 3200\ кг $$ \(Ответ:\ N =\ 40\ Вт\) |
3. Определите кинетическую энергию пули массой \(15\ г\), вылетевшей из ружья вертикально вверх со скоростью \(650\ м/с\).
|
\(Дано:\)
\(m = 15\ г = 15 \cdot 10^{-3}\ кг\) \(v = 650\ м/с\) \(Найти: E_k = ?\) |
\(Решение:\)
Используем формулу кинетической энергии: $$E_k = \frac{mv^2}{2} = \frac{15 \cdot 10^{-3} \cdot 650^2}{2} = 3168.75\ Дж $$ \(Ответ: E_k = 3168.75\ Дж\) |
4. Найти кинетическую энергию стрелы массой \(0,5\ кг\), пущенную вертикально вверх со скоростью \(30\ м/с\) через \(2\ с\) после начала движения.
|
\(Дано:\)
\(m = 0.5\ кг\) \(v_0 = 30\ м/с\) \(t = 2\ с\) \(g = 10\ м/с^2\) Найти: \(E_k = ?\) |
\(Решение:\)
Движение вертикальное вверх: \(v = v_0 - gt\) \(v = 30 - 10 \cdot 2 = 10\ м/с\) Теперь $$ E_k = \frac{mv^2}{2} = \frac{0.5 \cdot 10^2}{2} = 25\ Дж $$ \(Ответ: E_k = 25\ Дж\) |
5.Тело массой \(300\ г\) летит вертикально вверх на высоту \(90\ метров\). Чему равна потенциальная энергия тела на этой высоте?
|
\(Дано:\)
\(m = 300\ г\ =\ 0.3\ кг\) \(h = 90\ м\) Найти: \(E_p = ?\) |
\(Решение:\)
Находим по основной формуле потенциальной энергии: $$E_p\ =\ mgh\ =\ 0.3 \cdot 10 \cdot 90\ =\ 270\ Дж$$ \(Ответ: E_p = 270\ Дж\) |
6. Чему равно отношение потенциальных энергий пружин, если первая пружина имеет жесткость \(40\ Н/м\), вторая \(50\ Н/м\), обе пружины растянулись на \(5\ см\)?
|
\(Дано:\)
\(k_1\ =\ 40\ Н/м\) \(k_2\ =\ 50\ Н/м\) \(x\ =\ 5\ см\) Найти: \(\frac{E_{p1}}{E_{p2}} = ?\) |
\(Решение:\)
Находим формуле потенциальной энергии для деформированной пружины: \(E_p\ =\ \frac{kx^2}{2}\) $$ \frac{E_{p1}}{E_{p2}}\ =\ \frac{k_1 x^2}{2} : \frac{k_2 x^2}{2} =\ \frac{k_1}{k_2} = \frac{40}{50} \ = 0.8 $$ \(Ответ: 0.8\) |
7. Камень массой \(2\ кг\) брошен вертикально вверх, его начальная кинетическая энергия \(250\ Дж\). На какой высоте скорость камня будет равна \(10\ м/с\)?
|
\(Дано:\)
\(m\ =\ 2\ кг \) \(E_{k0}\ =\ 250\ Дж\) \(v\ =\ 10\ м/с \) Найти: \(h = ?\) |
\(Решение:\)
По закону сохранения энергии, полная механическая энергия всегда постоянна. Давайте найдем его для начальной точки по формуле \(E\ =\ E_{k0}\ +\ E_{p0}\) Так как в самом начале движения тела находится на земле, то \(h_0\ =\ 0 \quad \Rightarrow \quad E_{p0}\ =\ mgh_0\ =\ 0\) $$E\ =\ E_{k0}\ +\ E_{p0} =\ 250\ +\ 0\ = 250\ Дж$$ Теперь перейдем к точке в которой скорость равна \(10\ м/с\). Кинетическая энергия для этой точки будет найдена по формуле \(E_k\ =\ \frac{mv^2}{2}\). А потенциальная энергия \(E_p\ =\ mgh\) $$ E =\ E_p\ +\ E_k\ = \frac{mv^2}{2} +\ mgh \quad \Rightarrow \quad mgh\ =\ E\ -\ \frac{mv^2}{2} \quad \Rightarrow \quad h\ =\ \frac{E\ -\ \frac{mv^2}{2}}{mg}$$ $$h\ =\ \frac{250\ -\ \frac{2 \cdot 10^2}{2}}{2 \cdot 10}\ =\ 7.5\ м$$ \(Ответ:\ h\ =\ 7.5\ м\) |