Импульс тела. Импульс силы. Закон сохранения импульса. Реактивное движение

Основные термины:

• импульс тела, импульс силы
• Закон сохранения импульса
• Абсолютно упругий удар
• Абсолютно неупругий удар
• Реактивное движение

Импульс тела \(p\) - векторная физическая величина, равная произведению массы тела на его скорость: $$ \vec{p} = m \vec{v} \quad \quad \quad \quad \quad [ кг \cdot м/с ] $$ Направление импульса совпадает с направлением скорости \(p \uparrow \uparrow v\). Импульс тела равен нулю, если тело не движется \(v = 0\)
Изменение импульса тела - векторная разность между конечным и начальным импульсом тела. \(\Delta \vec{p} = \vec{p} - \vec{p_0} = m \vec{v} - m \vec{v_0}\)
Изменение скорости осуществляется за счет наличия ускорения полученного силам действующим на тело. Попробуем вывести второй закон Ньютона.$$ \vec{F} = m \vec{a} = m \frac{ \vec{v} \ -\ \vec{v_0}}{\Delta t} \quad \quad \Rightarrow \quad \quad \vec{F} \cdot \Delta t = m( \vec{v} \ -\ \vec{v_0}) \quad \quad \Rightarrow \quad \quad \vec{F} \cdot \Delta t = \Delta \vec{p}$$ Величина \(\vec{F} \cdot \Delta t = \Delta \vec{p} \quad \) - импульс силы.
Импульс результирующей силы действующей на тело равна изменению его импульса. Отсюда видно что импульс тела изменяется под действием данной силы одинаково у тел любой массы, если только время действия сил одинаково.
Суммарный (полный) импульс системы тел - векторная сумма всех тел системы.
$$\vec{p} = \vec{p_1} + \vec{p_2} + \dots + \vec{p_n} = \Sigma \vec{p_i}$$
\(n\ –\ число\ тел\ в\ системе,\ i\ –\ порядковый\ номер\ тела,\ \Sigma –\ знак\ суммы\)

Закон сохранения импульса. Импульс замкнутой системы взаимодействующих тел остается величиной постоянной, если геометрическая сумма внешних сил, действующих на тела системы, равна нулю. Отсюда вывод. Суммарный импульс тел системы до взаимодействия равен суммарному импульсу тел после взаимодействия. $$\Sigma \vec{p_i} = const$$

Удар - тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь. При ударе выполняется закон сохранения импульса.

Абсолютно упругий удар

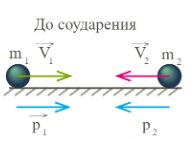
Абсолютно упругий удар - модель соударения, при котором сохраняется полная кинетическая энергия системы. Хороший пример абсолютно упругого удара столкновение бильярдных шаров или упругих мячиков. Для примера возьмем систему из двух тел: шары массами \(m_1\) и \(m_2\) равномерно и прямолинейно движутся со скоростями \( \vec{v_1} \ и\ \vec{v_2}\). Импульсы шаров записываются \(\vec{p_1}\ =\ m_1 \vec{v_1}, \quad \quad \vec{p_2} = m_2 \vec{v_2} \quad\) соответственно. 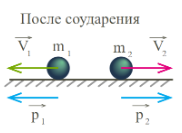Когда шары приблизятся друг к другу, произойдет столкновение. После столкновения модули и направления скоростей могут быть совершенно иными, поэтому обозначим скорости \( \vec{v_1}' \ и\ \vec{v_2}'\) соответственно. Изменятся и импульсы шаров, они станут равны \(\vec{p_1}'\ =\ m_1 \vec{v_1}', \quad \quad \vec{p_2}'\ =\ m_2 \vec{v_2}'\) Тогда, согласно закону сохранения импульса получаем следующее равенство: $$\vec{p_1} + \vec{p_2} = \vec{p_1}' + \vec{p_2}'$$ $$m_1 \vec{v_1} + m_2 \vec{v_2} = m_1 \vec{v_1}' + m_2 \vec{v_2}'$$ Это математическая запись закона сохранения импульса при абсолютно упругом ударе. !Импульсы складываются векторно.

Абсолютно неупругий удар

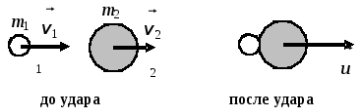
Абсолютно неупругий удар - удар, в результате которого, тела соединяются и продолжают дальнейшее свое движение как единое целое.$$m_1 \vec{v_1} + m_2 \vec{v_2} = (m_1 + m_2) \vec{u}$$ \(m_1 \ и\ m_2 \ -\ массы\ тел\) \(v_1 \ и\ v_2 \ -\ скорости\ тел\ до\ удара\) \(u\ -\ общая\ скорость\ тел\ после\ удара\)

Как и при любом ударе, при абсолютно неупругом ударе выполняется закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соударяемых тел в результате неупругих деформаций переходит в тепловую.

Реактивное движение

Реактивное движение - это вид движения, которое возникает при отделении от тела некоторой его части с определенной скоростью. Реактивные двигатели эффективны для случаев когда нет опоры для передвижения. Чтобы изменять свое положение в пространстве телу необходима точка опоры или сила, которая придает импульс. В безвоздушном пространстве импульс можно получить только от энергии реактивного движения.

Ракета - аппарат двигающийся за счёт реактивной силы вследствие выброса рабочего тела аппарата без использования веществ окружающей среды. Большую часть ракеты занимает топливо и окислитель. Для сгорания топлива необходим кислород (как известно в космосе его нет), поэтому для поддержания горения и необходим окислитель. Насосы подают топливо и окислитель в камеру сгорания. Горение топлива создает горячий газ с большим значением давления и скорости. Сопло ракеты направлено так, что газ вырывается противоположно направления её движения, тем самым придавая импульс ракете . Это можно показать с помощью закона сохранения импульса. Для упрощения расчёта параметров полёта не учитывают силы земного притяжения. Начальный импульс ракеты до старта равен нулю. Поэтому суммарный импульс движущейся ракеты и испускаемого газа тоже равен нулю. Это возможно только в противоположно направленном движении оболочки ракеты и струи газа: $$ p_{оболочки}\ =\ p_{топлива}$$ $$ \left( M_{ракеты} \ -\ m_{топлива} \right) v \ =\ m_{топлива} v_{топлива}$$ $$ v = \frac{m_{топлива} v_{топлива}}{M_{ракеты} \ -\ m_{топлива}}$$

Примеры решения задач

1. Мотоциклист массой \(67\ кг\) имеет импульс, модуль которого равен \(598\ кг \cdot м/с\). Вычисли скорость мотоциклиста.

\(Дано:\) \(m = 67\ кг\) \(p = 598\ кг \cdot м/с\) Найти: \(v = ?\)

\(Решение:\) Формула импульса тела \(p\ =\ mv\) Преобразуем ее для нахождения скорости: $$ v\ =\ \frac{p}{m} \ =\ \frac{598}{67} \ =\ 8.9\ м/с $$ \(Ответ: v = 8.9\ м/с\)

2. Шарик массой \(M\ =\ 16\ кг\) движется со скоростью \(19\ м/с\), а шарик с массой \(m\ =\ 8\ кг\) движется со скоростью \(6\ м/с\) вдоль оси \(Ox\). Определите значения проекций импульсов обеих шариков.

\(Дано:\) \(M = 16\ кг\) \(v_1 = 19\ м/с\) \(m = 8\ кг\) \(v_2 = 6\ м/с\) Найти: \(p_1 = ?\) \(p_2\ =\ ?\)

\(Решение:\) Формула импульса тела \(p\ =\ mv\) Не забываем что знак проекции зависит от направления движения тела, поэтому будет так: $$p_{1x}\ =\ p_1\ =\ Mv_1\ =\ 16 \cdot 19\ =\ 304\ кг \cdot м/с$$ $$p_{2x}\ =\ - p_2\ =\ -mv_2\ =\ - 8 \cdot 6\ =\ - 48\ кг \cdot м/с$$ \(Ответ: p_1 = 304\ кг \cdot м/с, \quad p_2\ =\ - 48\ кг \cdot м/с\)

3. Тележка массой \(40\ кг\) движется со скоростью \(4\ м/с\) навстречу тележке массой \(60\ кг\), движущейся со скоростью \(2\ м/с\). После неупругого соударения тележки движутся вместе. В каком направлении и с какой скоростью будут двигаться тележки?

\(Дано:\) \(m_1 = 40\ кг\) \(v_1 = 4\ м/с\) \(m_2 = 60\ кг\) \(v_2 = 2\ м/с\) Найти: \(u = ?\)

\(Решение:\) Уравнение закона сохранения импульса для неупругого удара: \(m_1 \vec{v_1} + m_2 \vec{v_2} = (m_1 + m_2) \vec{u}\) В проекции на ось \(Ox\) с учетом направлением будет: \(m_1v_1 \ -\ m_2v_2\ =\ (m_1 + m_2) \cdot u\) Мы взяли правильным направление первого тела, если полученная скорость \(u\) будет положительной, то движение направлено так же. А если отрицательное, то противоположно к нему и сонаправлено с направлением тела второго тела до удара. Выразим скорость \(u\) после удара: $$u\ =\ \frac{m_1v_1 \ -\ m_2v_2}{m_1\ +\ m_2}\ =\ \frac{40 \cdot 4 - 60 \cdot 2}{40 + 60}\ =\ \frac{40}{100} = 0.4\ м/с$$ \(Ответ: u = 0.4\ м/с\)

4. В проплывающую под мостиком лодку массой \(150\ кг\) опускают с мостика груз массой \(50\ кг\). Какова будет после этого скорость лодки, если ее начальная скорость \(4\ м/с\)?

\(Дано:\) \(m_1 = 150\ кг\) \(m_2 = 50\ кг\) \(v_1 = 4\ м/с\) \(v_2 = 0\ м/с\) Найти: \(u = ?\)

\(Решение:\) После "удара" тела движутся вместе, так как человек становится на лодку. Поэтому это можно интерпретировать как неупругий удар, уравнение которого выглядит как: \(m_1 \vec{v_1} + m_2 \vec{v_2} = (m_1 + m_2) \vec{u}\) С учетом направления движения первого тела и тем что скорость второго тела была нулевой: \(m_1v_1 = (m_1 + m_2)\cdot u\) $$ u\ =\ \frac{m_1v_1}{m_1\ +\ m_2}\ =\ \frac{150 \cdot 4}{150 + 50}\ =\ \frac{600}{200} = 3\ м/с$$ \(Ответ: v = 3\ м/с\)

5. С какой скоростью истекал газ при запуске модели космического корабля массой \(200\ г\), если максимальная высота его подъема составила \(12,8\ м\)? При запуске модели было использовано \(0,5\ кг\) горючего, сопротивлением воздуха пренебречь.

\(Дано:\) \(M = 200\ г =\ 0.2\ кг\) \(h = 12.8\ м\) \(m = 0.5\ кг\) Найти: \(v_{топлива} = ?\)

\(Решение:\) Тело поднималось наверх двигаясь равнозамедленно. С помощью уравнения движения тела и движения скорости мы можем найти начальную скорость ракеты. $$h = v_0t - \frac{gt^2}{2}$$ $$v = v_0 - gt$$ Тело поднимается наверх пока его скорость не станет равной нулю. Поэтому: $$0 = v_0 - gt \quad \quad \Rightarrow \quad \quad t = \frac{v_0}{g}$$ $$h = v_0 \cdot \frac{v_0}{g} - \frac{g\cdot (v_0 \\ g)^2}{2} = \frac{v_0^2}{g} - \frac{v_0^2}{2g} = \frac{v_0^2}{2g} $$ $$v_0 = \sqrt{2gh} = \sqrt{2\cdot 10 \cdot 12.8}\ =\ 16\ м/с$$ Вернемся к движению ракеты и закону сохранения импульса. Основное уравнение \( M_{ракеты}v \ =\ m_{топлива} v_{топлива}\) $$v_{топлива} = \frac{M_{ракеты}v}{m_{топлива}} = \frac{0.2 \cdot 16}{0.5} = 6.4\ м/с$$ \(Ответ: v_{топлива} = 6.4\ м/с\)