Свет. Скорость света. Волновые свойства

Свет — форма электромагнитного излучения, видимая человеческим глазом. Является одним из основных источников энергии и информации о внешнем мире.

Скорость света ($c$) — константа, равная примерно 299,792 км/с в вакууме. Это максимальная возможная скорость распространения информации и энергии во Вселенной.

Скорость света связывает длину волны $ \lambda $ и период колебаний $ T $:

$$ c = \frac{\lambda}{T} = \lambda \cdot \nu $$

Показатель преломления $ n $ вещества характеризует его оптические свойства:

$$ n = \frac{c}{v} $$

где $ v $ — скорость света в веществе.

Для любых двух сред:

$$ \frac{v_1}{v_2} = \frac{n_2}{n_1} $$

Связь между скоростью света, длиной волны и частотой:

$$ v = \lambda \cdot \nu $$

Так как $ \nu = \text{const} $ при переходе света между средами, то:

$$ \frac{\lambda_1}{\lambda_2} = \frac{v_1}{v_2} = \frac{n_2}{n_1} $$

Длина световой волны в веществе:

$$ \lambda_n = \frac{\lambda}{n} $$

Волновые свойства света проявляются в:

интерференции
дифракции
дисперсии
поляризации

Фазовая скорость — скорость распространения фазы волны в пространстве.

Когерентность — свойство источников испускать волны с постоянной разностью фаз.

Интерференция — наложение двух или более волн, вызывающее усиление или ослабление результирующей волны.

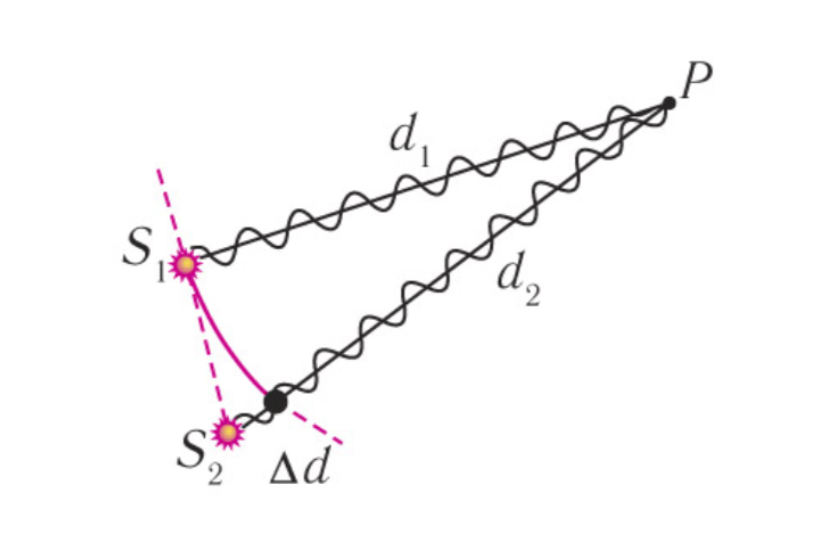
Если в точку P приходят две волны с разными путями $ d_1 $ и $ d_2 $:

$$ \Delta d = d_2 - d_1 $$

Разность фаз:

$$ \Delta \varphi = \frac{2\pi}{\lambda} \cdot \Delta d $$

Условия интерференции

Максимум (синфазно): $ \Delta d = m\lambda $, $ m = 0,1,2... $
Минимум (противофазно): $ \Delta d = (2m + 1) \frac{\lambda}{2} $

Если волны проходят среды с показателями преломления $ n_1 $, $ n_2 $:

Оптическая разность хода:

$$ \delta = n_2 d_2 - n_1 d_1 $$

Максимум: $ \delta = m \lambda $
Минимум: $ \delta = (2m + 1) \frac{\lambda}{2} $

Дифракция — огибание препятствий или прохождение через узкие отверстия, вызывающее распределение интенсивности света в пространстве.

Принцип Гюйгенса: каждая точка волнового фронта становится источником вторичных волн. Новый фронт — огибающая этих волн.

Дифракционная решётка — система из $ N $ равноотстоящих щелей.

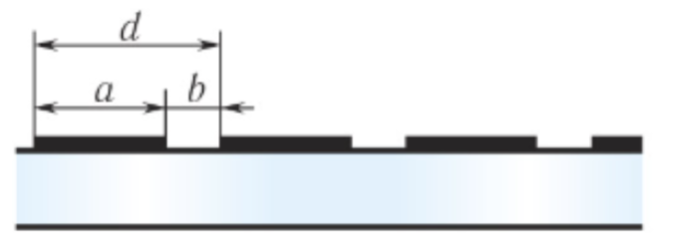
Условие главных максимумов при нормальном падении света:

$$ d \cdot \sin \theta = m \lambda \quad (m = 0,1,2,...) $$

Поляризация — упорядоченная ориентация вектора электрического поля $ \vec{E} $ световой волны в одном направлении.

Дисперсия — зависимость скорости света в веществе от частоты (или длины волны):

$$ v = \frac{c}{n(\nu)} $$

Или:

$$ n = n(\lambda) $$

Призма преломляет разные длины волн по-разному, создавая спектр:

Цвет	Длина волны, нм
Красный	770–630
Оранжевый	630–590
Жёлтый	590–570
Зелёный	570–495
Голубой/Синий	495–435
Фиолетовый	435–390

Примеры решения задач

1. Что будет наблюдаться в некоторой точке пространства в результате интерференции двух когерентных волн длиной волны $\lambda$ = 400 нм, оптическая разность хода которых $\delta$ = 2.25 мкм?

$Дано:$
$\lambda = 400\ нм = 4 \cdot 10^{-7}\ м$
$\delta = 2{,}25\ мкм = 2{,}25 \cdot 10^{-6}\ м$
Найти: максимум / минимум

$Решение:$
Интерференционный минимум наблюдается, если оптическая разность хода: $$\delta = (2m + 1) \cdot \frac{\lambda}{2}$$ Найдём $m$: $$m = \frac{\delta}{\lambda} = \frac{2{,}25 \cdot 10^{-6}}{4 \cdot 10^{-7}} = 5{,}625$$ Так как значение нецелое и попадает между двумя минимумами, то в точке наблюдается интерференционный минимум (ослабление).
$Ответ:$ минимум

2.На дифракционную решётку падает нормально свет с длиной волны 590 нм. Найти угол, под которым наблюдается максимум 6-го порядка. Период решётки 37 мкм. Ответ получить в градусах.

$Дано:$
$\lambda = 590\ нм = 5{,}9 \cdot 10^{-7}\ м$
$d = 37\ мкм = 3{,}7 \cdot 10^{-5}\ м$
$m = 6$
Найти: $\theta$

$Решение:$
При нормальном падении света на дифракционную решётку условие максимумов: $$d \cdot \sin \theta = m \lambda$$ Подставим значения: $$ \sin \theta = \frac{m \lambda}{d} = \frac{6 \cdot 5{,}9 \cdot 10^{-7}}{3{,}7 \cdot 10^{-5}} \approx 0{,}0957 $$ $$ \theta = \arcsin(0{,}0957) \approx 5{,}5^\circ $$
$Ответ:\ \theta \approx 5{,}5^\circ$

3. Скорость распространения света в воде $v_1$ = 2.250 ⋅ 105 км/с, а в стекле — $v_2$ = 1.982 ⋅ 105 км/с. Определите отношение $k$ показателей преломления стекла и воды.

$Дано:$
Скорость в воде: $v_1 = 2{,}250 \cdot 10^5\ км/с$
Скорость в стекле: $v_2 = 1{,}982 \cdot 10^5\ км/с$
Найти: $k = \frac{n_2}{n_1}$

$Решение:$
Так как показатель преломления $n = \frac{c}{v}$, то: $$ \frac{n_2}{n_1} = \frac{v_1}{v_2} = \frac{2{,}250 \cdot 10^5}{1{,}982 \cdot 10^5} \approx 1{,}135 $$
$Ответ:\ k \approx 1{,}135$