Изменение агрегатного состояния вещества

Агрегатное состояние вещества — это физическое состояние вещества, зависящее от сочетания температуры и давления.

Возможные агрегатные состояния:

Твёрдое
Жидкое
Газообразное
Плазма (в курсе не рассматривается)

Газ — агрегатное состояние вещества, в котором:

Частицы (молекулы, атомы, ионы) слабо взаимодействуют;
Движение частиц хаотичное и почти свободное;
При столкновениях частицы резко меняют направление движения.

Жидкое состояние — промежуточное состояние между твёрдым телом и газом:

Частицы связаны между собой;
Жидкость может менять форму под действием малых касательных напряжений, не изменяя объём.

Твёрдое состояние — агрегатное состояние вещества, которое:

Имеет стабильную форму;
Частицы совершают малые колебания около положений равновесия.

Фазовый переход — это переход вещества из одного агрегатного состояния в другое с поглощением или выделением теплоты.
При этом молекулы вещества не изменяются, меняются только связи между ними.

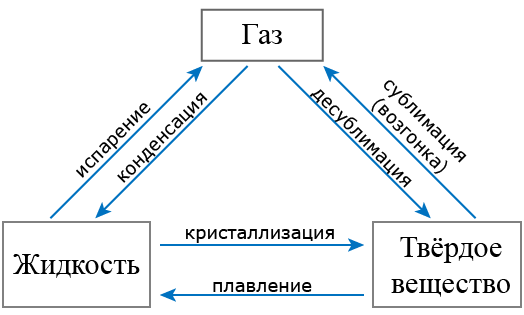
Конденсация — это обратный процесс испарения, то есть переход вещества из газообразного состояния в жидкое.

Испарение — переход вещества из жидкого состояния в газообразное.

Кристаллизация — переход вещества из жидкого состояния в твёрдое.

Плавление — обратный процесс: переход вещества из твёрдого состояния в жидкое.

Сублимация — переход вещества из твёрдого состояния сразу в газообразное, минуя жидкое состояние.

Десублимация — переход вещества из газообразного состояния сразу в твёрдое, минуя жидкую фазу.

Динамическое равновесие

Если сосуд закрыт, то устанавливается динамическое равновесие:

скорость испарения = скорости конденсации

Такая система называется двухфазной.

Формула парообразования/конденсации

(Процесс происходит при постоянной температуре):

$$ Q = Lm $$

где:

$ Q $ — количество теплоты,
$ L $ — удельная теплота парообразования (Дж/кг),
$ m $ — масса вещества (кг).

Насыщенный пар — это пар, находящийся в динамическом равновесии со своей жидкостью.

Формула кристаллизации/плавления

(Процесс происходит при постоянной температуре):

$$ Q = \lambda m $$

где:

$ Q $ — количество теплоты,
$ \lambda $ — удельная теплота плавления (Дж/кг),
$ m $ — масса вещества (кг).

Уравнение теплового баланса

Выводится из закона сохранения энергии:
Энергия изолированной системы сохраняется с течением времени.

Изолированная система — это система, не обменивающаяся с окружающей средой ни веществом, ни энергией.

Следовательно, в изолированной системе:

$$ Q_1 + Q_2 + \ldots + Q_n = 0 $$

где $ Q_i $ — количество теплоты, полученное или отданное ( i )-той частью системы:

$ Q > 0 $: получено
$ Q < 0 $: отдано

Формула для нагревания тела

Для расчёта количества теплоты, необходимого для нагревания тела:

По удельной теплоёмкости:

$$ Q = cm\Delta T $$

где:

$ Q $ — количество теплоты.
$ c $ — удельная теплоёмкость вещества (Дж/кг·°C),
$ m $ — масса тела (кг),
$ \Delta T $ — изменение температуры (°C),

По молярной теплоёмкости:

$$ Q = \nu\Delta T m_\nu $$

где:

$ m_\nu $ — молярная теплоемкость материала $\frac{Дж}{моль}$, можно узнать из таблиц ,
$ \nu $ — количество вещества в молях.
$\Delta T$-изменение температуры (с учетом знака)

Пример задач

1. Какое количество теплоты нужно подвести к 10 г льда при температуре 200 К, чтобы превратить их в 10 г водяного пара при температуре 400 К?

$ Дано: $
$ m = 10 \ \text{г} = 0{,}01 \ \text{кг} $
$ T_1 = 200 \ \text{K} $, $ T_2 = 400 \ \text{K} $
$ c_л = 2100 \ \frac{\text{Дж}}{\text{кг·К}} $,
$ c_в = 4200 \ \frac{\text{Дж}}{\text{кг·К}} $,
$ c_п = 2200 \ \frac{\text{Дж}}{\text{кг·К}} $,
$ \lambda = 333 \cdot 10^3 \ \frac{\text{Дж}}{\text{кг}} $,
$ L = 2{,}3 \cdot 10^6 \ \frac{\text{Дж}}{\text{кг}} $
$ Найти: Q = ? $

$ Решение: $
Процесс состоит из пяти этапов:
1) Нагревание льда: \[ Q_1 = c_л \cdot m \cdot (273 - 200) = 2100 \cdot 0{,}01 \cdot 73 = 1533 \ Дж \] 2) Плавление льда: \[ Q_2 = \lambda \cdot m = 333000 \cdot 0{,}01 = 3330 \ Дж \] 3) Нагрев воды: \[ Q_3 = c_в \cdot m \cdot (373 - 273) = 4200 \cdot 0{,}01 \cdot 100 = 4200 \ Дж \] 4) Парообразование: \[ Q_4 = L \cdot m = 2300000 \cdot 0{,}01 = 23000 \ Дж \] 5) Нагрев пара: \[ Q_5 = c_п \cdot m \cdot (400 - 373) = 2200 \cdot 0{,}01 \cdot 27 = 594 \ Дж \] Суммарное количество теплоты: \[ Q = Q_1 + Q_2 + Q_3 + Q_4 + Q_5 = 1533 + 3330 + 4200 + 23000 + 594 = 32657 \ Дж = 32{,}657 \ кДж \] $ Ответ: Q = 32{,}657 \ кДж $

2. В замкнутой системе смешали 1 л воды при температуре 293K и 2 л воды при температуре 303K. Какая температура установится после теплообмена?

$ Дано: $
$ V_1 = 1 \ л, \ T_1 = 293 \ K $
$ V_2 = 2 \ л, \ T_2 = 303 \ K $
$ c_в = 4200 \ \frac{\text{Дж}}{\text{кг·К}} $, $ \rho = 1000 \ \frac{\text{кг}}{\text{м}^3} $
$ Найти: T_c = ? $

$ Решение: $
Используем закон сохранения энергии: \[ c \cdot m_1 \cdot (T_c - T_1) = c \cdot m_2 \cdot (T_2 - T_c) \] \[ m_1 = 1 \ \text{кг}, \ m_2 = 2 \ \text{кг} \Rightarrow T_c = \frac{m_1 \cdot T_1 + m_2 \cdot T_2}{m_1 + m_2} = \frac{1 \cdot 293 + 2 \cdot 303}{1 + 2} = \frac{899}{3} \approx 299{,}67 \ \text{K} \] $ Ответ: T_c \approx 300 \ K $

3. Определите удельную теплоту сгорания топлива, если для нагрева 25 л воды от 20°C до 85°C сожгли 900 г топлива. КПД нагревания — 50%.

$ Дано: $
$ V = 25 \ л = 25 \ кг $
$ T_1 = 293 \ K, \ T_2 = 358 \ K $
$ c_в = 4200 \ \frac{\text{Дж}}{\text{кг·К}} $
$ m_{\text{топл}} = 0{,}9 \ \text{кг} $,
$ \eta = 0{,}5 $
$ Найти: q = ? $

$ Решение: $
Тепло, полученное водой: \[ Q = c \cdot m \cdot (T_2 - T_1) = 4200 \cdot 25 \cdot (358 - 293) = 4200 \cdot 25 \cdot 65 = 6825000 \ Дж \] Учтём КПД: \[ \eta = \frac{Q}{q \cdot m_{\text{топл}}} \Rightarrow q = \frac{Q}{\eta \cdot m_{\text{топл}}} = \frac{6825000}{0{,}5 \cdot 0{,}9} \approx 15166666{,}7 \ \frac{\text{Дж}}{\text{кг}} = 15{,}17 \cdot 10^6 \ \frac{\text{Дж}}{\text{кг}} \] $ Ответ: q \approx 15{,}2 \cdot 10^6 \ \frac{\text{Дж}}{\text{кг}} $ — соответствует сухим дровам.