Газовые законы

Идеальный газ — модель газа, обладающая следующими характеристиками:

1. Состоит из отдельных молекул.
2. Молекулы не взаимодействуют на расстоянии (взаимодействуют только при столкновении как упругие шарики).

Уравне́ние состоя́ния — соотношение, отражающее для конкретного класса термодинамических систем связь между макроскопическими физическими величинами: температура, давление, объем, химический потенциал, энтропия, внутренняя энергия, энтальпия и др.

Уравне́ние состоя́ния идеального газа — соотношение, отражающее связь между температурой, давлением, объемом и количеством вещества.

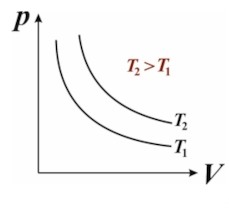
Закон Бойля–Мариотта

Для данного, не меняющегося количества идеального газа, произведение давления газа на занимаемый им объём при постоянной температуре — постоянно:

$$ P V = \text{const} \quad (T = \text{const}) $$

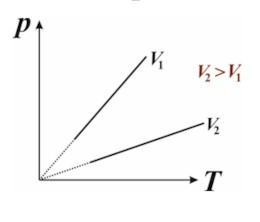
Закон Шарля

Для данного количества идеального газа, отношение давления к абсолютной температуре при постоянном объёме — постоянно:

$$ \frac{P}{T} = \text{const} \quad (V = \text{const}) $$

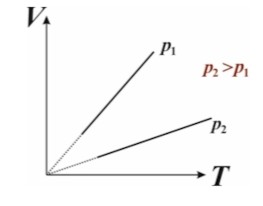
Закон Гей-Люссака

Для данного количества идеального газа, отношение объема к температуре при постоянном давлении — постоянно:

$$ \frac{V}{T} = \text{const} \quad (P = \text{const}) $$

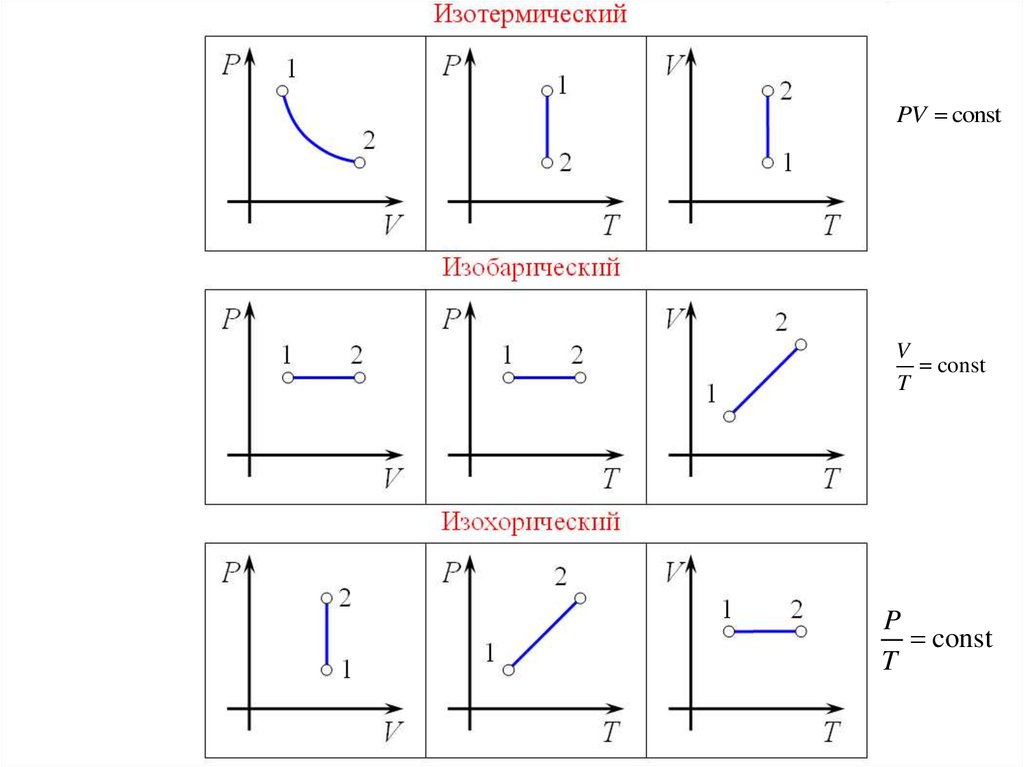
Изопроцессы — это термодинамические процессы, при которых одно из параметров состояния (P, V или T) остаётся неизменным, а также количество вещества не меняется.

Закон Клапейрона (Менделеева–Клапейрона)

Для данного количества идеального газа произведение давления на объём прямо пропорционально температуре:

$$ P V = \nu R T $$

где:

• \( P \) — давление (Па)
• \( V \) — объём (м³)
• \( T \) — абсолютная температура (К)
• \( \nu \) — количество вещества (моль)
• \( R = 8.31 \ \text{Дж/(моль·К)} \) — универсальная газовая постоянная

Количество вещества через массу и молярную массу:

$$ \nu = \frac{m}{M} $$

Тогда уравнение принимает вид:

$$ P V = \frac{m}{M} R T $$

Закон Дальтона

Закон Дальтона описывает давление в газовых смесях. Он гласит, что общее давление смеси равно сумме парциальных давлений всех газов в смеси.

Парциальное давление — давление, которое оказывал бы каждый газ, если бы он один занимал весь объём смеси при той же температуре.

Формула закона Дальтона:

$$ P = P_1 + P_2 + P_3 + \dots + P_n $$

где:

• \( P \) — общее давление смеси
• \( P_1, P_2, \dots, P_n \) — парциальные давления отдельных газов

Пример задач

1.В закрытом недеформируемом сосуде нагревают газ от температуры 20 градусов цельсия до 40 градусов цельсия. Начальное давление было равно 1 атм. Каково давление в сосуде в конце процесса. В качестве ответа дать формулу, по которой можно оценить давление, и число – давление в атм.

2. В закрытом тонкой пленкой сосуде (давление в сосуде всегда равно атмосферному) нагревают газ от температуры 0 градусов Цельсия до 40 градусов Цельсия. Начальный объем равен \( 1 \ \text{м}^3 \). Какой объем занимает газ в конце процесса? В качестве ответа дать формулу, по которой можно оценить объем, и число – объем в \( \text{м}^3 \).

3.В закрытом сосуде с поршнем, при постоянной температуре, проводят процесс при которов объем сосуда уменьшается в 2 раза. Если давление в начале процесса было равно 2 атм, чему равно давление в конце процесса. В качестве ответа дать формулу, по которой можно оценить давление, и число – давление в Па.