Простые механизмы. Условие равновесия рычага. КПД.

Основные термины:

• Простые механизмы
• Рычаг
• Неподвижный блок
• Подвижный блок

Средства, используемые для преобразования силы и изменения его направления, называются простыми механизмами. Они позволяют совершать работу без применения источников не механической энергии.
К простым механизмам относятся рычаг, блок, наклонная плоскость и их разновидности: ворот, клин и винт.
Золотое правило механики С помощью простого механизма нельзя получить выигрыш в работе. Во сколько раз мы выигрываем в силе, во столько раз мы проигрываем в расстоянии.
Рычаг - это тело, имеющее ось вращения, к которому приложены силы, поворачивающие его относительно оси вращения. Рычаг позволяет меньшей силой уравновесить большую силу. Рычаги бывают первого и второго рода, в зависимости от точки опоры.

$$Рис. 1\ Рычаг\ первого\ рода.$$	$$Рис. 2\ Рычаг\ второго\ рода.$$
$$F_1 \cdot l_1\ =\ F_2 \cdot l_2$$ \(O\ -\ точка\ опоры\) \(l_1\ -\ длина\ плеча\ OA\) \(l_2\ -\ длина\ плеча\ OB\) \(F_1,\ F_2\ -\ действующие\ силы\)

Выигрыш в силе для рычага рассчитывается по соотношению длин плеч \(n\ =\ \frac{F_2}{F_1}\ =\ \frac{l_1}{l_2}\)

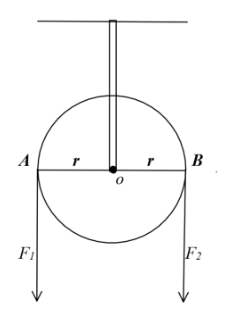
Неподвижный блок - это небольшое колесо, закрепленное на неподвижной оси. Неподвижный блок изменяет направление силы, но не изменяет ее величину. $$r\ -\ длина\ плеча\ OA$$ $$r\ -\ длина\ плеча\ OB$$ $$F_1,\ F_2\ -\ действующие\ силы $$ $$F_1 \cdot r\ =\ F_2 \cdot r$$ $$F_1\ =\ F_2$$

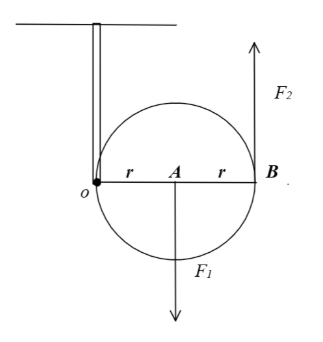
Подвижный блок - это подвижное колесо, которое дает выигрыш в силе в 2 раза и меняет его направление. $$r\ -\ длина\ плеча\ OA$$ $$2r\ -\ длина\ плеча\ OB$$ $$F_1,\ F_2\ -\ действующие\ силы $$ $$F_1 \cdot r\ =\ F_2 \cdot 2r$$ $$F_1\ =\ 2F_2$$

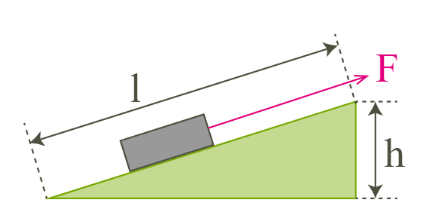
Наклонная плоскость - является простым механизмом, который используют для того, чтобы сэкономить силу при вертикальном перемещении различных грузов. Чем больше является отношение длины плоскости к ее высоте, тем больше экономия в силе. Если длина наклонной плоскости \(l\) и высота \(h\), тогда экономия в силе будет в \(n\ =\ \frac{l}{h}\) раз. $$A_{совершенная}\ =\ F \cdot l$$ $$A_{полезная}\ =\ mgh$$

КПД наклонной плоскости.

КПД (коэффициентом полезного действия) - называют отношение полезной работы к полной работе.
\(A_{пол}\) – «полезная работа » – работа, которую необходимо выполнить;
\(A_{сов}\) – «полная работа» – работа, которую совершили;
\( \eta \) – коэффициент полезного действия (\( \eta \) – греческая буква, читается «эта») $$ \eta \ =\ \frac{А_{пол}}{А_{сов}}$$ Коэффициент полезного действия выражается чаще не в долях от целого, а в процентах. Для этого отношение полезной работы к совершенной умножают на 100% $$ \eta \ =\ \frac{А_{пол}}{А_{сов}} \cdot 100 % $$

**1. На рычаге размещены два противовеса таким образом, что рычаг находится в состоянии равновесия. Вес расположенного слева противовеса равен \(P_1\ =\ 70\ Н\). Какой вес \(P_2\) расположенного справа противовеса, если все обозначенные на перекладине рычага участки имеют одинаковую длину? **

\(Дано:\) \(P_1 = 70\ Н\) \(d_1\ =\ 9d\) \(d_2\ =\ 1d\) \(Найти: P_2 = ?\)

\(Решение:\) Длину одного обозначенного участка на перекладине отметим как \(d\). Тогда \(d_1\ =\ 9d\) и \(d_2\ =\ 1d\). Не забываем что сила тяжести начинается по центру фигур. Раз уж рычаг находится в равновесии то момент силы действующий по направлению часовой стрелки равна моменту силы действующий против направления часовой стрелки. Формула момента силы: \(M\ =\ F\cdot d\ =\ P \cdot d\) \(\quad \quad \quad P_1\cdot d_1 \ =\ P_2\cdot d_2 \quad \quad \Rightarrow \quad \quad P_2\ =\ \frac{P_1 d_1}{d_2} =\ \frac{70 \cdot 9d}{d} \ =\ 630\ Н\) \(Ответ: P_2 \ =\ 630\ Н\)

2. К концам стержня массой \(10\ кг\) и длиной \(40\ см\) подвешены грузы массами \(40\ кг\) и \(10\ кг\). Где необходимо подпереть стержень, чтобы он находился в равновесии.

\(Дано:\) \(m\ =\ 10\ кг\) \(m_1\ =\ 40\ кг\) \(m_2\ =\ 10\ кг\) \(l\ =\ 40\ см\) Найти: \(x = ?\)

\(Решение:\) Пусть \(х\) - расстояние от левого конца стержня (где висит груз \(40\ кг\) ) до точки опоры. Раз уж стержень находится в равновесии то момент силы действующий по направлению часовой стрелки равна моменту силы действующей против направления часовой стрелки. С обеих сторон помимо сил тяжестей грузов действуют еще и сила тяжести части стержня. Не забываем что центр силы тяжести будет ровно в середине этой части стержня. 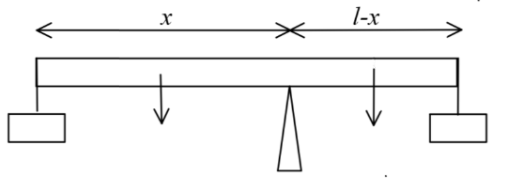Для начала найдем силу тяжести частей стержня. Так как это твердое плотное тело, масса части будет пряма пропорциональна длине части. Масса левой части стержня \(m_{лев}\ =\ \frac{m \cdot x}{l}\) Масса правой части стержня \(m_{прав}\ =\ \frac{m \cdot (l - x)}{l}\) Формула момента силы действующей против часовой стрелки: \(M_{против}\ =\ M_1 + M_2 \ =\ m_1 gx + \frac{mgx}{l} \cdot \frac{x}{2}\) Формула момента силы действующей по часовой стрелке: \(M_{по}\ =\ M_1 \ +\ M_2 \ =\ m_2 g(l-x)\ +\ \ \frac{mg(l-x)}{l} \cdot \frac{(l-x)}{2}\) \(m_1 gx + \frac{mgx}{l} \cdot \frac{x}{2} \ =\ m_2 g(l-x)\ \frac{mg(l-x)}{l} \cdot \frac{(l-x)}{2}\) умножаем это на \(2l\) \(2lm_1x\ +\ mx^2 \ =\ 2lm_2(l - x)\ +\ m(l - x)^2\) \(2lm_1x\ +\ mx^2 \ =\ 2lm_2(l - x)\ +\ ml^2\ -\ 2mlx\ +\ mx^2\) Сокращаем \(mx^2\) и все делим на \(l\) \(2m_1x\ =\ 2m_2(l - x)\ +\ ml\ -\ 2mx\) \(2m_1x\ +\ 2m_2x\ +\ 2mx\ =\ ml\ +\ 2m_2l\) \(2x(m_1\ +\ m_2\ +\ m)\ =\ l(m\ +\ 2m_2)\) \(x\ =\ \frac{l(m\ +\ 2m_2)}{2(m_1\ +\ m_2\ +\ m)}\ =\ \frac{0.4 \cdot (10\ +\ 2 \cdot 10)}{2 \cdot (10\ +\ 40\ +\ 10)}\ =\ 0.1\ м\) \(Ответ: x = 0.1\ м\)

3. Для подъёма груза по наклонной плоскости приложили силу, направленную вдоль наклонной плоскости и равную \(300\ Н\). Найдите массу груза, если известно, что длина наклонной плоскости равна \(1,5\ м\), а её высота равна \(1\ м\).

4.Груз массой \(15\ кг\) равномерно перемещают по наклонной плоскости, прикладывая при этом силу в \(40\ Н\). Чему равно КПД наклонной плоскости, если длина ее \(1,8\ м,\) а высота — \(30\ см\)?.