Уравнение неразрывности и уравнение Бернулли. Подъемная сила.

Основные термины:

• идеальная жидкость
• уравнение Неразрывности
• уравнением Бернулли
• подъемная сила крыла

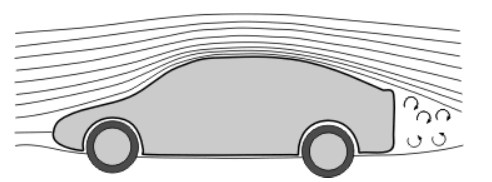
Гидро- и аэродинамика – это раздел механики, изучающий движение жидкостей и газов, а также взаимодействие движущихся жидкостей и газов с твердыми телами. К задачам гидродинамики относятся вычисление подъемной силы и силы сопротивления, действующих на движущееся тело. Для упрощения решения задач гидродинамики введены понятия «идеальная жидкость», «элемент тока».

Идеальная жидкость – это жидкость, вязкостью и сжимаемостью которой можно пренебречь.

Элемент тока – это условно выделенный малый объем жидкости (газа), изменением формы которого при движении можно пренебречь.

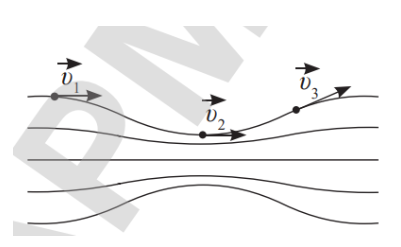
Один из способов изучения движения жидкости заключается в следующем: в жидкость подмешивают металлические блестки и делают фотоснимок с малой выдержкой при сильном освещении. На снимке блестки выглядят как черточки, длины которых пропорциональны скорости течения жидкости. По направлению движения блесток можно судить о направлении течения жидкости в любой точке ее поверхности. При увеличении выдержки фотосъемки черточки сливаются в сплошные линии, которые называют линиями тока. Таким методом изучал течение жидкости Эйлер. Линии тока – это линии, касательные к которым совпадают по направлению со скоростью течения жидкости в соответствующих точках пространства.

Трубка тока – это объем жидкости или газа, ограниченный линиями тока. Скорость жидкости или газа в каждой точке линии тока направлена по касательной, следовательно, жидкость, находящаяся внутри трубки тока, не пересекает ее боковой поверхности.

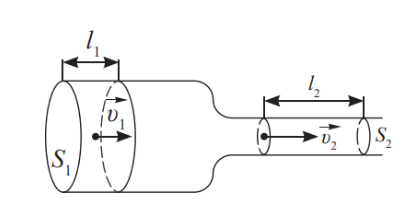
Рассмотрим два сечения трубки тока площадями \(S_1\) и \(S_2\) с соответствующими скоростями движения жидкости \(v_1\) и \(v_2\) . Пусть движение жидкости в трубке стационарное. При стационарном движении все частицы проходят точки пространства с соответствующими им скоростями. За промежуток времени \( \Delta t\) через сечение \(S_1\) проходит жидкость объемом \(V_1 = S_1 \cdot l_1 = S_1 \cdot v_1t.\) Через второе сечение \(S_2\) за это же время: \(V_2 = S_2 \cdot l_2 = S_2 \cdot v_2t.\) Для несжимаемой жидкости \(V_1 = V_2\) , следовательно: $$ S_1 v_1 = S_2 v_2 \quad \quad \quad или \quad \quad \quad \frac{v_1}{v_2} = \frac{S_2}{S_1}$$ Получено соотношение, которое называют уравнением неразрывности. Модули скоростей несжимаемой жидкости обратно пропорциональны площадям сечения трубок тока.

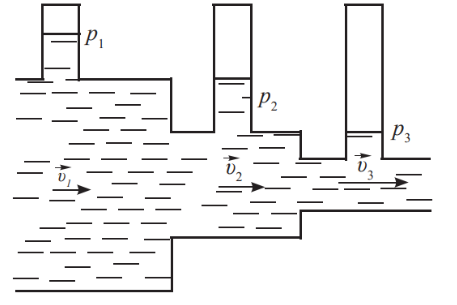
Определим давление жидкости в трубе переменного сечения с помощью жидкостных манометров. Опыт показывает, что в широких частях трубы давление больше, чем в узких. На основании уравнения неразрывности следует, что в той части трубы, где сечение больше, скорость течения меньше. При стационарном течении жидкости давление больше в той части трубы, где скорость течения меньше. Зависимость давления жидкости от скорости ее стационарного течения в математической форме была установлена швейцарским физиком Даниилом Бернулли в 1738 г. Закон сохранения энергии в применении к движущейся в трубке идеальной жидкости получил название уравнения Бернулли. $$p_1 + \rho gh_1 + \frac{\rho v_1^2}{2} = p_2 + \rho gh_2 + \frac{\rho v_2^2}{2}$$ $$p + \rho gh + \frac{\rho v^2}{2} = const. $$

Выражения выше и называют уравнением Бернулли для идеальной жидкости или законом сохранения плотности энергии для движущихся жидкостей и газов. Согласно уравнению Бернулли:

Подъемная сила крыла.
Основным приспособлением, служащим для изучения законов движения тел в воздухе, является аэродинамическая труба. В одном конце трубы установлен мощный вентилятор, приводимый во вращение электродвигателем . В них исследуют не только модели, но и реальные самолеты. Аэродинамические трубы изготавливают различных размеров.

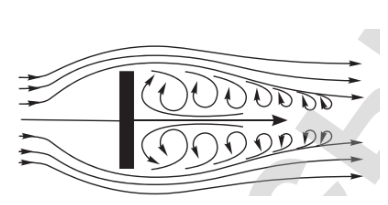
На рисунке представлена картина обтекания пластины, плоскость которой направлена перпендикулярно потоку, созданному в аэродинамической трубе. Плотность воздуха перед пластиной возрастает, за пластиной – уменьшается. Воздух устремляется в разреженное пространство и создаёт завихрения. При этом пластина не перемещается по вертикали.

Если между пластиной и потоком воздуха образуется острый угол, то разность давлений создает аэродинамическую силу, пластина поднимается или опускается. Угол наклона назван углом атаки, его обозначают греческой буквой \( \alpha \). Аэродинамическая сила возникает не только за счет угла атаки, она создается несимметричным профилем крыла. Над крылом скорость потока больше, чем под крылом, благодаря тому, что верхняя часть более выпуклая. Согласно уравнению Бернулли, давление на нижнюю часть крыла больше, чем над крылом.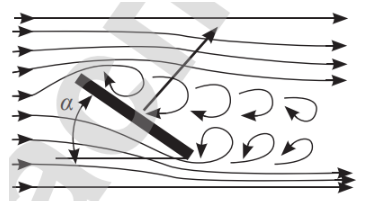

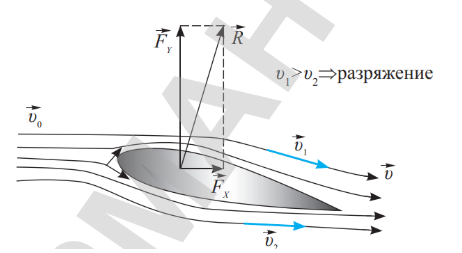
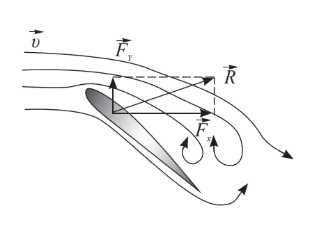
Чем больше скорость набегающего на крыло потока, тем больше разность давлений и аэродинамическая сила \(R\), которую можно разложить на подъемную силу \(F_y\) и силу лобового сопротивления \(F_x\). С увеличением угла наклона подъемная сила возрастает, лобовое сопротивление уменьшается. При критическом значении угла атаки происходит отрыв потока от поверхности крыла, подъемная сила пропадает, сила сопротивления резко возрастает. Самолет входит в «штопор»

Примеры решения задач:

1. В горизонтальной трубе газопровода диаметром \(40\ см\) течет газ со скоростью \(50\ см/с.\) Труба сужается и газ стал двигаться со скоростью \(1,75\ м/с.\) Каким стал диаметр трубы?

2. Вода течет в трубе переменного сечения. В сечении с площадью \(15\ см^2\) скорость потока воды \(2\ м/с\), а скорость потока в сечении площадью \(10\ см^2\) равна?

3. В широкой части горизонтальной трубы вода течет со скоростью 8 см/с при давлении, равном \(1,5 \cdot 10^5\ Па\). В узкой части трубы давление равно \(1,4 \cdot 10^5\ Па.\) Определите скорость течения в узкой части трубы без учета трения.

4. Определите скорость полета струи воды из шприца диаметром \(4\ см\), на поршень которого действует сила \(30\ Н\). Площадь отверстия шприца много меньше площади поршня, сопротивлением воздуха пренебречь.