Формула Торричелли. Формула Стокса.

Основные термины:

• Формулыа Стокса
• Вязкость
• Формула Торичелли
• Коэффициент скорости

Движение тел в жидкостях и газах. Формула Стокса.
При движении тел в жидкостях и газах возникают силы сопротивления. Они вызваны двумя причинами:

1. трением среды о поверхность тела;
2. изменением потока жидкости или газа при обтекании тела.
   Сила лобового сопротивления среды зависит от вязкости среды, а также от скорости движения тела, его размеров и формы. Сила лобового сопротивления, которую испытывает шарик, падающий в вязкой жидкости или газе, определяется формулой Стокса, названной в честь английского физика, внесшего значительный вклад в гидродинамику, Джорджа Габриеля Стокса: $$F = 6 \pi \eta rv$$ \(\eta −\ коэффициент\ внутреннего\ трения\ жидкости\ или\ газа\ или\ динамическая\ вязкость,\ единица\ измерения\ [\eta]\ –\ [Па \cdot с];\)
   \(r\ –\ радиус\ шарика;\)
   \(v\ −\ скорость\ шарика;\)
   
   Формула Стокса позволяет определить вязкость жидкостей. Приборы, созданные для определения вязкости жидкостей, называют вискозиметрами. Действие вискозиметра Гепплера основано на законе Стокса, он представляет собой трубку, в которую помещается вязкая среда. Вязкость определяется по скорости прохождения падающим шариком промежутков между метками на трубке вискозиметра, который позволяет вести измерения с погрешностью в пределах от 1 до 3 %.
   

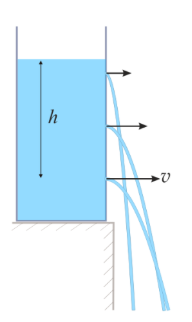
Формула Торричелли, формула для скорости истечения жидкости из отверстия в открытом сосуде: $$v = \sqrt{2gh}$$ \(где\ h\ —\ высота\ уровня\ жидкости,\ отсчитываемая\ от\ центра\ отверстия;\) \(g\ —\ ускорение\ силы\ тяжести;\) Впервые установлена Э. Торричелли в 1641. Из Т. ф. следует, что скорость истечения жидкости из отверстия одинакова для всех жидкостей и зависит лишь от высоты, с которой жидкость опустилась, то есть равна скорости свободного падения тела с той же высоты. Действительная же скорость истечения несколько отличается от скорости, определяемой формулой Торричелли: она зависит от формы и размера отверстия, от вязкости жидкости и от величины расхода. Для учёта этих обстоятельств в формулу вводят поправочный множитель , меньший единицы; тогда формула приобретает вид: $$v = \phi \sqrt{2gh}$$ \( \phi \ называется\ коэффициентом\ скорости\ при\ истечении\ жидкости\ из\ отверстия;\) для малого круглого при больших Рейнольдса числах он равен \(0,94 — 0,99.\) Значения для отверстий других форм и размеров приводятся в гидравлических справочниках.

Примеры решения задач:

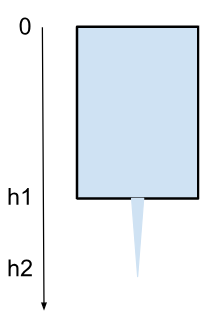
**1. На дне бака высотой \(50\ см\), полностью заполненного водой, имеется отверстие площадью \(1\ см^2\) значительно меньшей площади сечения бака. Если открыть отверстие, то из него начинает вытекать струя воды. Чему равна площадь сечения струи на высоте \(20\ см\) ниже дна бака? **

\(Дано:\) \(h_1 = 50\ см\ = 0.5\ м\) \(S_1 = 1\ см^2 = 1 \cdot 10^{-4}\ м^2\) \(\Delta h = 20\ см\ = 0.2\ м\) \(Найти: S_2 = ?\)

\(Решение:\) По формуле Торричелли мы можем найти значение скорости на каждой из высот. \(v = \sqrt{2gh}\) $$v_1 = \sqrt{2gh_1} = \sqrt{2 \cdot 10 \cdot 0.5} \approx 3.16\ м/с$$ $$v_2 = \sqrt{2gh_2} = \sqrt{2g (h_1 + \Delta h)} = \sqrt{2 \cdot 10 \cdot (0.5\ +\ 0.2)} \approx 3.74\ м/с$$ В дано задачи сказано что вода стекает, соответственно она течет не под напором, поэтому уменьшается как скорость движения струи так и площадь поперечного сечения. По уравнению неразрывности: $$S_1v_1 = S_2 v_2 \quad \quad \Rightarrow \quad \quad S_2 = \frac{S_1 v_1}{v_2} = \frac{10^{-4} \cdot 3.16}{3.74} \approx 0.84\ см^2$$ \(Ответ: S_2 = 0.84\ см^2\)

2. В водопроводной трубе образовалось отверстие сечением \(4\ мм^2\), из которого вертикально вверх бьет струя воды, поднимаясь на высоту \(80\ см\). Какова утечка воды за сутки?