Давление. Гидростатическое давление. Атмосферное давление. Закон Паскаля.

Основные термины:

• Давление
• Гидростатическое давление
• Закон Паскаля
• Атмосферное давление
• Нормальное атмосферное давление
• Ртутный барометр
• Манометр

Давление твердых тел.

Давление \(p\) — величина, равная отношению силы \(F\), действующей перпендикулярно поверхности, к площади этой поверхности \(S\). $$p\ =\ \frac{F}{S} \quad \quad \quad \quad \quad \quad [Па]$$ За единицу давления принимают давление, которое производит сила \(1\ Н\), действующая на перпендикулярную поверхность площадью \(1\ м^2\).
Увеличить давление можно, увеличивая силу давления или уменьшая площадь опоры. Все колющие и режущие инструменты: иголки, ножницы, ножи, имеют малую площадь острия или резца. Это позволяет малой силой создать большое давление. Давление уменьшится, если уменьшить силу давления или увеличить площадь опоры. Именно поэтому гусеницы трактора, шины вездехода имеют большую площадь поверхности. Как показывают расчеты, давление, которое создает человек своим весом, в десятки раз превышает давление вездехода. В твердых телах давление передается по направлению действия силы.

Давление в жидкостях и газах.

В жидкостях давление передается во всех направлениях благодаря свойству текучести. Дно сосуда испытывает давление, созданное весом жидкости: \(F_д\ =\ P\ =\ mg\). Учитывая, что \(m\ =\ \rho \cdot V,\ а\ V\ =\ S \cdot h\) получим формулу расчета давления внутри жидкости: \(\quad F_д\ =\ \rho Shg\) $$p\ = \frac{F}{S}\ =\ \frac{\rho Shg}{S} = \rho gh$$
Давление вызванное весом жидкости называется гидростатическим. Гидростатическое давление жидкости зависит от высоты столба жидкости и ее плотности. Оно не зависит от площади основания сосуда.
Жидкости, обладая свойством текучести, передают давление во всех направлениях. Следовательно, давление на одном и том же уровне жидкости в различных направлениях должно быть одинаковым.
Давление в газах создается ударами молекул. Для увеличения давления газа необходимо увеличить число ударов о поверхность тела. Для этого необходимо увеличить плотность газа или повысить его температуру. При увеличении плотности газа число молекул в единице объема возрастет, число ударов о поверхность тела в единицу времени станет больше. При повышении температуры молекулы газа будут двигаться быстрее, число ударов возрастет, сила удара увеличится.
В газах давление передается по всем направлениям благодаря свойству газа равномерно заполнять весь предоставленный ему объем.

Закон Паскаля. Давление, производимое на жидкость или газ, передается без изменения в каждую точку объема жидкости или газа.

Воздушную оболочку Земли называют атмосферой. Атмосферное давление – давление атмосферы на поверхность Земли и на тела, находящиеся внутри воздушной оболочки.

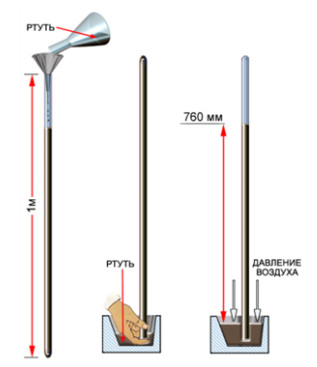
Рассчитать давление воздуха так же, как давление в жидкости, невозможно по двум основным причинам: у атмосферы нет определенной границы, ее плотность с высотой меняется. Впервые измерить атмосферное давление удалось итальянскому ученому Эванджелиста Торричелли. Наполнив трубку длиной \(1\ м\) ртутью, он опустил ее открытым концом в чашу со ртутью. Часть ртути вылилась в чашу, а часть осталась в трубке. Высота оставшейся ртути в проведенных опытах была всегда близка значению \(76\ см.\) Э. Торричелли дал следующее объяснение опыту. Атмосфера давит на поверхность ртути в чаше. Ртуть находится в равновесии. Значит, по закону Паскаля, давление в трубке на уровне ртути в чаше равно атмосферному давлению. В верхней части трубки воздуха нет, поэтому давление в трубке создается только ртутью. Отсюда следует, что атмосферное давление равно давлению столба ртути в трубке: $$p_{атм}\ =\ \rho_{рт} g h_{рт}$$

Наблюдая за ртутным столбом в трубке, Торричелли обнаружил, что его высота может меняться. Он заметил, что изменение давления связано с изменением погоды. Опытная установка Торричелли в дальнейшем использовалась как измерительный прибор для определения атмосферного давления. Прибор получил название ртутный барометр (от греч. \(baros\) – тяжесть, \(metro\) – измеряю). Шкала прибора градуируется в \(мм\) или \(см.\)

Найдем соотношение между единицами измерения. Определим давление ртути высотой \(1\ мм.\) $$ p\ =\ 13600 кг/м^3 \cdot 9,8\ Н/кг \cdot 0,001\ м \approx 133,3\ Па$$
Таким образом, связь единиц измерения давления, получивших практическое применение, следующая: \(1\ мм\ рт.\ ст.\ \approx \ 133,3\ Па\)

Дальнейшие исследования и расчеты физиков показали, что при подъеме на \(8\ м\) давление атмосферы уменьшается на \(1\ гПа.\) Выражая давление в \(мм\ рт.\ ст.\), получим следующее соотношение: давление атмосферы уменьшается на \(1\ мм\ рт.\ ст.\) при подъеме на высоту около \(11\ м.\)
Нормальным атмосферным давлением называют атмосферное давление, равное давлению столба ртути высотой \(760\ мм\) при температуре \(0°С.\) Выразим нормальное атмосферное давление в Па: \(760\ мм\ рт.\ ст.\ \approx 760 \cdot 133,3\ Па\ \approx \ 101300\ Па \ \approx 105\ Па.\)

Манометр – прибор для измерения давлений, больших или меньших атмосферного давления.

Примеры решения задач:

1. Книга лежит на столе. Масса книги равна \(0,6\ кг.\) Площадь ее соприкосновения со столом равна \(0,08 \ м^2.\) Определите давление книги на стол.

2. На горизонтальном полу лежит плита из бетона толщиной \(25\ см.\) Определите давление, производимое плитой.

3. Вычислите давление нефти на дно бака, если верхний уровень ее находится в \(9,5\ м\) от дна. Определите силу давления на дно бака, площадь которого равна \(290\ м^2\)