Волны. Длина волны. Звуковые волны. Эхо

Волны — распространение колебаний в упругой среде, сопровождающееся переносом энергии, но не вещества.

Длина волны \( \lambda \) — расстояние между двумя ближайшими точками, колеблющимися в одной фазе (например, двумя гребнями волны).

Формула:
$$ \lambda = vT $$ где:

• \( \lambda \) — длина волны,
• \( v \) — скорость распространения волны,
• \( T \) — период волны.

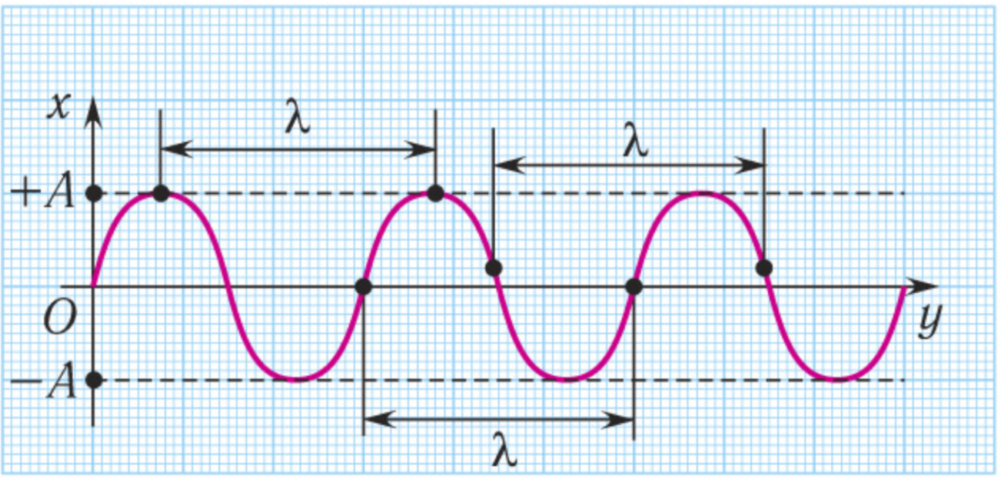
Скорость распространения волны \( v \) — скорость, с которой волна перемещается в среде.

Формула:
$$ v = \lambda f $$ где \( f \) — частота волны.

Упругие механические волны — волны, которые распространяются за счёт упругих свойств среды. Пример: звуковые волны в газах, жидкостях и твердых телах.

Звуковые волны — тип упругих механических волн, воспринимаемых слухом. Возникают при колебаниях частиц среды и распространяются через неё.

Скорость звука - зависит от среды:

• в воздухе (при 20 °C): \( \approx 343\ \text{м/с} \)
• в воде: \( \approx 1500\ \text{м/с} \)
• в стали: \( \approx 5000\ \text{м/с} \)

Высота звука — зависит от частоты колебаний. Чем выше частота, тем выше высота звука.

Громкость звука — зависит от амплитуды колебаний. Бóльшая амплитуда — более громкий звук.

Эхо — отражение звуковой волны от препятствия.
Для расчета расстояния до препятствия:

$$ s = \frac{v t}{2} $$

где:

• \( s \) — расстояние до препятствия,
• \( v \) — скорость звука,
• \( t \) — время от исходного звука до его эха.

Период \( T \) — время одного полного колебания.

$$ T = \frac{\tau}{N} $$
где:

• \( \tau \) — общее время,
• \( N \) — число колебаний.

Частота \( f \) — число колебаний в секунду:
$$ f = \frac{1}{T} $$ Единица измерения: герц (Гц).

Продольные волны — колебания происходят вдоль направления распространения волны.

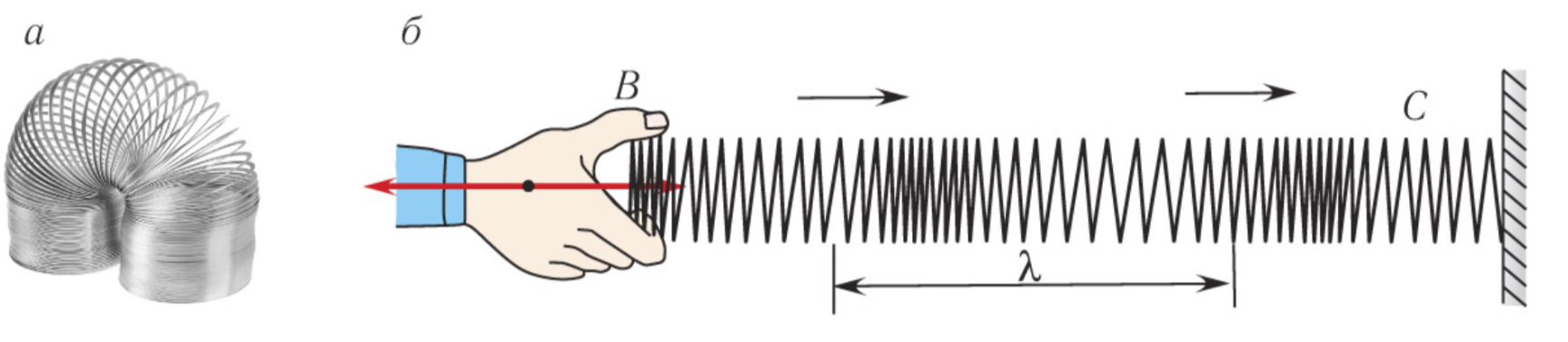
Поперечные волны - колебания происходят перпендикулярно направлению распространения волны.

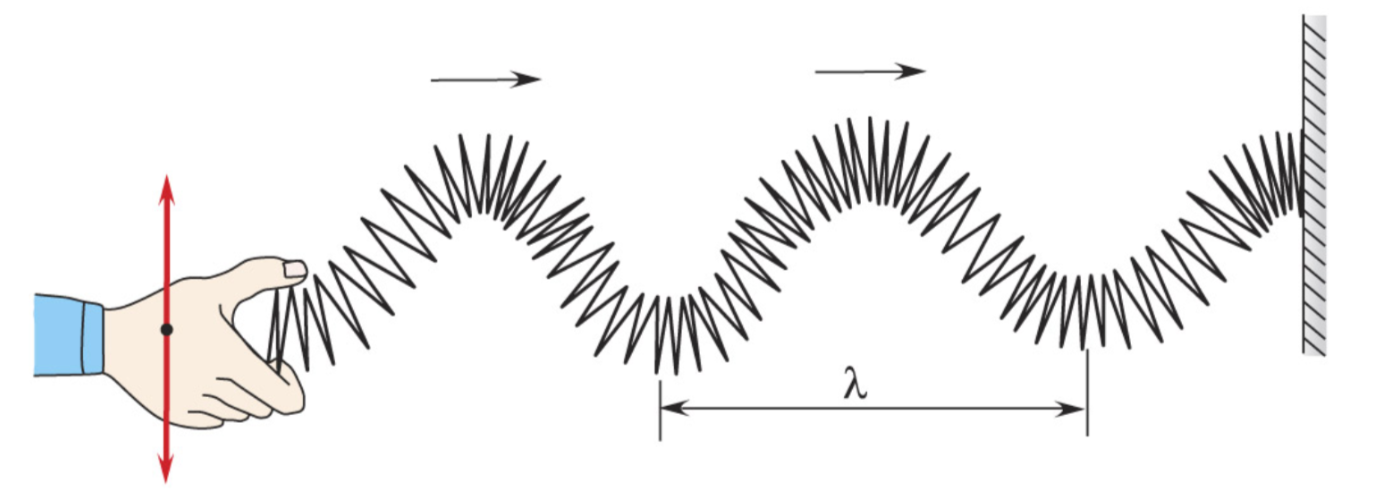
Амплитуда — максимальное отклонение от положения равновесия. Определяет энергию и громкость волны.

Примеры решение задач:

1. Определите модуль скорости распространения волны, если её длина \( \lambda = 15\ \text{м} \), а период колебаний \( T = 0{,}20\ \text{с} \)

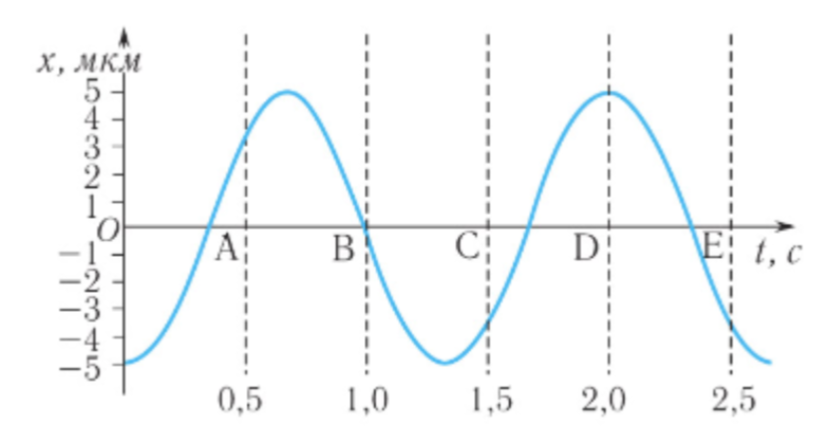
2. Определите амплитуду и период колебаний по графику

\( Дано:\) График волны (см. рисунок)

\( Решение:\) По вертикальной оси определим амплитуду: \( A = 5\ мкм \) По горизонтальной оси видно, что период волны: \( T \approx 1{,}3\ \text{с} \) \( \textbf{Ответ: } A = 5\ мкм,\ T = 1{,}3\ \text{с} \)

3. Неподвижный наблюдатель за время \( \Delta t = 20\ \text{с} \) насчитал \( n = 8 \) гребней волн. Найти период колебаний частиц.