- +7 777 150 51 51
Свободные и вынужденные колебания. Гармонические колебания. Скорость и ускорение при гармонических колебаниях. Период, частота, амплитуда и фаза колебаний. Графики и уравнение электромагнитных гармонических колебаний
Движение, периодически повторяющееся во времени, называют колебательным движением.
Колебания, происходящие под действием внешней периодически изменяющейся силы, называют вынужденными колебаниями. Внешняя сила изменяет период колебания системы и вынуждает систему колебаться.
Свободные колебания – колебания в системе под действием внутренних сил, после того как система выведена из положения равновесия. Колебания груза, подвешенного на нити, или груза, прикрепленного к пружине, – это примеры свободных колебаний. После выведения этих систем из положения равновесия создаются условия, при которых тела колеблются без воздействия внешних сил. Систему тел, способную совершать свободные колебания, называют колебательной системой.
Простейшим типом колебаний являются гармонические колебания. Это такие движения, когда физические величины изменяются по закону синуса или косинуса.
Положение равновесия – это устойчивое состояние колебательной системы.
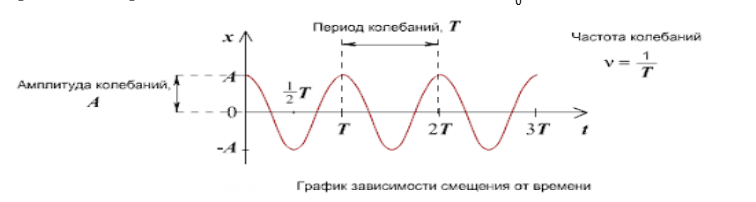
Шарик на нити, смещаясь от положения равновесия, проходит расстояние от одной точки максимального отклонения до другой и возвращается обратно. Расстояние от точки равновесия 0 до точки максимального отклонения называют амплитудой колебания, обозначают буквой \(А\), измеряют в метрах.
Период \(T\) – это время, за которое совершается одно полное колебание системы.
$$T = \frac{t}{N}$$
\(t\ -\ время\ колебаний, \)
\(N\ -\ количество\ совершенных\ колебаний\)
Совершая колебания, тело каждую точку траектории проходит дважды.
Частота \(\nu\) – это количество колебаний, совершенных системой за единицу времени.
$$\nu = \frac{N}{t}$$
Связь между периодом и частотой: \(\nu = \frac{1}{T} \quad \quad \quad T = \frac{1}{\nu}\)
Циклическая частота \(\omega\) – это число колебаний, совершенных за \(2 \pi\) секунд.
$$\omega = 2 \pi \nu = \frac{2 \pi}{T} \quad \quad \quad \quad [\frac{рад}{с}]$$
Фаза колебаний \(varphi\) это величина, определяющая состояние колебательной системы.
$$\varphi = \omega t = 2 \pi \nu \cdot t = \frac{2 \pi t}{T}$$
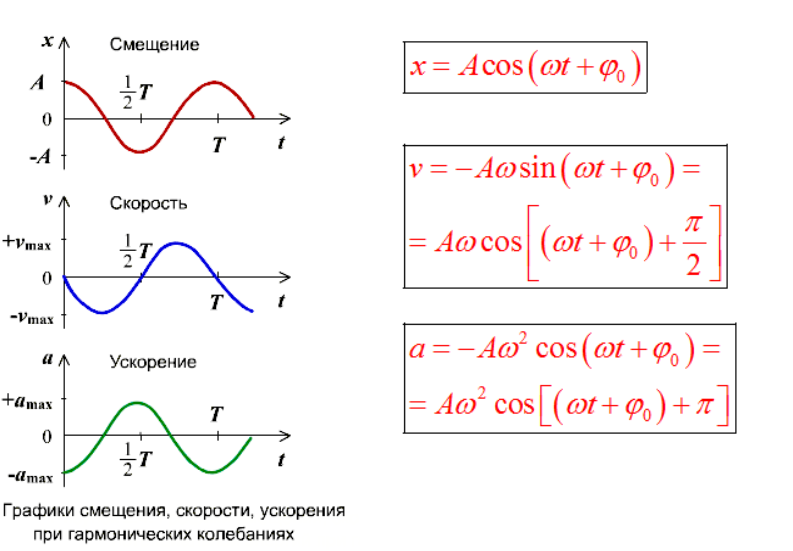
Уравнение гармонических колебаний:
$$x = A cos (\omega t + \varphi_0)$$
Скорость при гармонических колебаниях определяется как производная координаты \(x\) от времени \(t\) : $$ v = x' = -A \omega sin(\omega t + \varphi_0 ) = - v_{max} sin(\omega t + \varphi_0) $$
$$v_{max} = A \omega = 2 \pi \nu \cdot A = \frac{2 \pi \cdot A}{T}$$
Ускорение при гармонических колебаниях определяется как производная координаты \(v\) от времени \(t\):
$$a = v' = -A \omega^2 cos(\omega t + \varphi_0 ) = - a_{max} cos(\omega t + \varphi_0)$$
$$a_{max} = A \omega^2 = 4 \pi^2 \nu^2 \cdot A = \frac{4 \pi^2 \cdot A}{T^2}$$
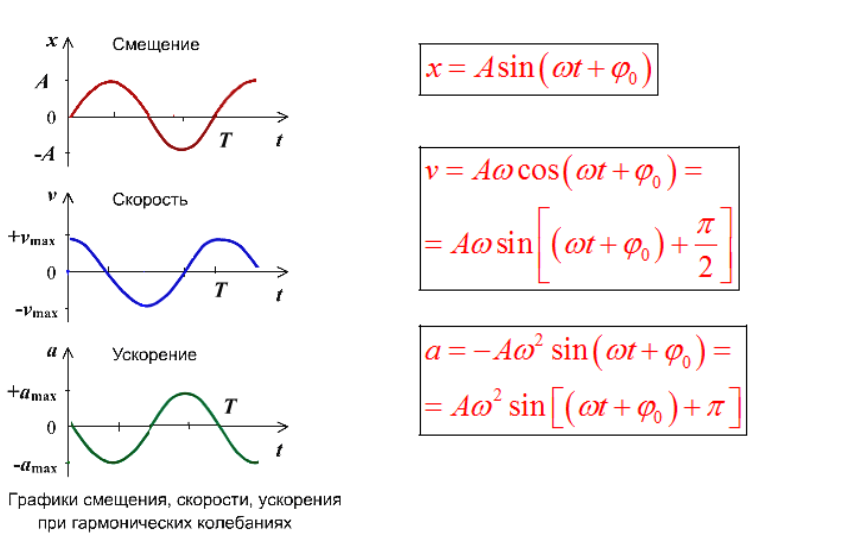
Начальная фаза гармонического колебания влияет на форму его математического описания, но принципиально любое гармоническое колебание можно записать либо через синус, либо через косинус, потому что эти функции отличаются лишь сдвигом по фазе. Уравнения скорости и ускорения действительно будут отличаться знаком и фазой в зависимости от формы записи (через синус или косинус), но все они описывают одну и ту же физику. Основным считается уравнение по косинусу так как в большинстве физических систем (например, маятник, пружина), объект в начальный момент времени часто запускается с максимального отклонения и с нулевой скоростью. Это соответствует косинусоидальной форме.
Примеры решения задач:
1.Сколько колебаний совершит материальная точка за \(5\ с\) при частоте колебаний \(440\ Гц\)?
|
\(Дано:\)
\(t = 5\ с\) \(\nu = 440\ Гц\) \(Найти: N = ?\) |
\(Решение:\)
Частота находится по формуле $$\nu = \frac{N}{t}$$ Преобразуем ее: $$N = \nu \cdot t = 440 \cdot 5 = 2200$$ \(Ответ: 2200\) |
2.Материальная точка за \(1\ мин\) совершила \300\) колебаний. Определить период и частоту колебаний.
|
\(Дано:\)
\(t = 1\ мин = 60\ c\) \(N = 300\) \(Найти: \nu, T = ?\) |
\(Решение:\)
Частота находится по формуле $$\nu = \frac{N}{t} = \frac{300}{60} = 5\ Гц$$ А период: $$T = \frac{t}{N} = \frac{60}{300} = 0.2\ с$$ \(Ответ: 5\ Гц, 0,2\ с\) |
3.Напишите уравнение гармонических колебаний, если частота равна 0,5 Гц, а амплитуда 80 см.
|
\(Дано:\)
\(\nu = 0.5\ Гц \) \(A = 80\ см = 0,8\ м\) \(Найти: x = ?\) |
\(Решение:\)
Уравнение гармонических колебаний в общем виде: $$x = A cos (\omega t + \varphi_0)$$ Значение амплитуды известно, а циклическую частоту найдем по формуле: $$\omega = 2 \pi \nu = 2 \cdot \pi \cdot 0.5 = \pi$$ $$x = A cos (\omega t + \varphi_0) = 0.8 \cdot cos (\pi t + 0) = 0.8 cos \pi t$$ |