lessons.kz
Физика ЕНТ
Магнитное поле
Сила Ампера. Сила Лоренца. Контур с током в магнитном поле.

Сила Ампера. Сила Лоренца. Контур с током в магнитном поле.

Силу, с которой магнитное поле действует на проводник с током, называют силой Ампера. Модуль силы Ампера вычисляется по формуле: $$F_A = B Il\ sin \alpha$$ $F_A - Сила\ Ампера\ [Н];$
$B - магнитная\ индукция\ поля\ [Тл];$
$I - сила\ тока\ в\ проводнике\ [А];$
$l - длина\ проводника\ в\ магнитном\ поле\ [м];$
$\alpha - угол\ между\ направлением\ тока\ в\ проводнике\ и\ вектором\ магнитной\ индукции.$

Направление силы Ампера определяется правилом левой руки. Если левую руку расположить так, чтобы вектор индукции $B$ входил в ладонь, а четыре вытянутых пальца указывали направление тока $I$, то отогнутый на $90°$ большой палец укажет направление силы Ампера $F$.

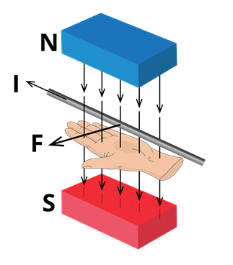
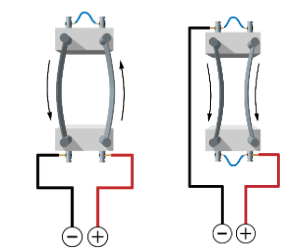
Взаимосвязь проводников с током.
Если по параллельным проводникам ток будет идти в одном направлении, то проводники будут подвержены силам притяжения. А если токи будут идти в противоположных направлениях, то проводники будут подвержены силам отталкивания. $$F = \frac{\mu \mu_0 I_1 I_2 l}{2 \pi R}$$ $F- сила\ между\ проводниками\ [Н];$
$I_1, I_2 - сила\ тока\ в\ проводниках\ [А];$
$l - длины\ проводников\ [м];$
$R - расстояние\ между\ проводниками\ [м];$
$\mu_0 = 4\pi \cdot 10^{-7}\ Н/м - магнитная\ постоянная;$
$\mu - магнитная\ проницаемость\ среды$

Сила Лоренца – это сила, которая действует со стороны магнитного поля на движущуюся в нем заряженную частицу. $$F_Л = qvB \cdot sin \alpha$$ $F_Л - сила\ Лоренца\ [Н];$
$q - модуль\ заряда\ [Кл];$
$v - скорость\ заряда\ [м/с];$
$B - магнитная\ индукция\ поля\ [Тл];$
$\alpha - угол\ между\ вектором\ скорости\ заряда\ и\ вектором\ магнитной\ индукции.$

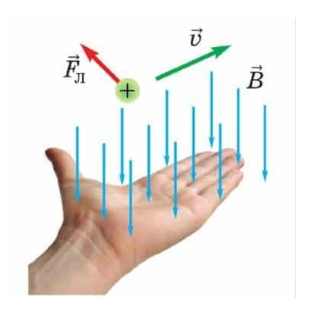
Направление силы Лоренца, действующей на положительную частицу, определяют по правилу левой руки.

Правило левой руки: Если левую руку расположить так, чтобы перпендикулярная к скорости частицы составляющая вектора индукции $В$ входила в ладонь, а четыре вытянутых пальца указывали направление движения заряда, то отогнутый на $90°$ большой палец покажет направление силы, действующей на этот заряд.

Если заряд отрицательный, то для определения направления силы Лоренца можно пользоваться тем же правилом, но в этом случае вектор силы Лоренца будет направлен противоположно отогнутому на $90°$ большому пальцу левой руки.

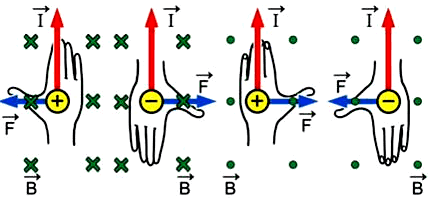
график

! Сила Лоренца сообщает движущемуся заряду только центростремительное ускорение. Она не изменяет величину скорости заряда и не совершает работу.

Наша Земля все время подвержена бомбардировке со стороны высокоэнергетических заряженных частиц, что представляет большую опасность для всей жизни на планете. Магнитное поле Земли их успешно экранирует, но все же бывают частицы, которые входят в магнитное поле Земли. И как только они входят в магнитное поле силы Лоренца уносят их параллельно линиям магнитной индукции Земли к полюсам Земли (явление «северное сияние»).

Движение заряженных частиц в магнитном поле. Возможны три случая заряженных частиц в магнитном поле.

1. Вектор $\vec{v}$ частицы параллелен к вектору магнитной индукции $\vec{B}.$ В этом случае заряженная частица движется в магнитном поле вдоль линий магнитной индукции. Угол а между векторами $\vec{v}$ и $\vec{В}$ равен нулю или $180°$. Так как в этом случае $sin \alpha = 0$, то сила Лоренца тоже равна нулю. Магнитное поле на частицу не действует, и она движется равномерно и прямолинейно.
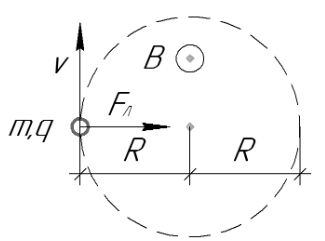
	2. Вектор $\vec{v}$ частицы перпендикулярен $(\alpha = 90°)$ к вектору магнитной индукции $\vec{B}$. В этом случае, поскольку сила Лоренца направлена перпендикулярно к скорости движения заряда, она создает частице центростремительное ускорение. Под действием силы Лоренца частица движется равномерно по окружности радиусом $R$: $$R = \frac{mv}{qB}$$ Период вращения: $$T = \frac{2\pi m}{Bq}$$
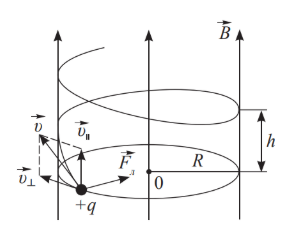
	Вектор $\vec{v}$ частицы направлен под некоторым углом $(\alpha \neq 90°)$ к вектору магнитной индукции $\vec{B}$. Если заряженная частица влетает в магнитное поле под некоторым углом $\alpha \neq 90°$, то она движется по винтовой траектории радиуса $R$ и шагом $h$., развивающейся на линии напряженности поля. В случае движения отрицательной частицы направление вращательного движения будет противоположным.

! Если заряженная частица одновременно движется в магнитном и электрическом полях, то на нее кроме силы Лоренца действует еще и электрическая сила.

Примеры решения задач:

1.Прямолинейный проводник с током длиной $l = 1\ м$, по которому течет ток $I = 1,5\ А$, находится в магнитном поле с индукцией $B = 0,1\ Тл$. Определите силу, действующую на проводник, если силовые линии магнитного поля расположены под углом $45°$ оси проводника.

$Дано:$
$l = 1\ м$
$I = 1.5\ А$
$B\ =\ 0.1\ Тл$
$ \alpha = 45°$

$Найти: F = ?$

$Решение:$
На проводник с током действует сила Ампера $$F_A = BIl sin \alpha = 0.1 \cdot 1.5 \cdot 1 \cdot \frac{\sqrt{2}}{2} \approx 0.1\ Н$$

$Ответ: 0,1\ Н$

2.В горизонтальном магнитном поле находится прямолинейный проводник, расположенный горизонтально и перпендикулярно линиям магнитной индукции. Какова сила тока, который должен течь в проводнике, чтобы сила натяжения в поддерживающих его проводах стала равной нулю? Магнитная индукция $B = 0,01\ Тл$. Отношение массы проводника к его длине $\frac{m}{l}=0.1 кг/м$.

$Дано:$
$B\ =\ 0.01\ Тл$
$\frac{m}{l}=0.1 кг/м$
$ \alpha = 90°$

$Найти: I = ?$

$Решение:$
На проводник с током действует сила Ампера, которая находится по формуле: $$F_A = BIl sin \alpha$$ Так же на тело действует сила тяжести самого проводника: $$F_т = mg$$ Сила натяжения со стороны поддерживающих проводов равна нулю, поэтому на тело действуют только эти силы. Направления у них противоположны, значит они должны быть равны друг другу так как: $$\vec{F_A} + \vec{F_т} = 0 \quad \quad \quad \quad \quad F_A - F_т = 0 \quad \quad \Rightarrow \quad \quad F_A = F_т$$ $$mg = BIl sin \alpha \quad \quad \Rightarrow \quad \quad I = \frac{mg}{Bl sin \alpha} = \frac{m}{l} \cdot \frac{g}{B sin \alpha}$$ $$I = \frac{m}{l} \cdot \frac{g}{B sin \alpha} = 0.1 \cdot \frac{10}{0.01 \cdot 1} = 100\ А$$

$Ответ: 100\ А$

3. Как взаимодействуют токи, направленные так, как указано в рисунке?

$Ответ:$ а) отталкиваются, так как ток течет в противоположных направлениях
б)притягиваются, так как ток течет в противоположных направлениях

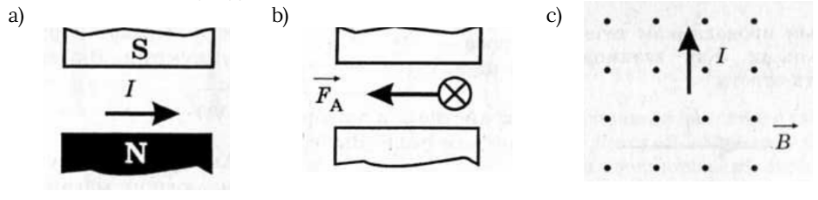
4. Дополните недостающие данные

$Ответ:$ а) Сила Ампера направленная к нам
b) нижнее-южный полюс магнита (S) , верхнее - северный полюс магнита (N)
c) Сила Ампера направленная направо

5.Точечный заряд $q = 2\cdot 10^{-6}\ Кл$ влетает со скоростью $v = 8\ м/с$ в однородное магнитное поле с индукцией $B = 0,25\ Тл$. Угол между скоростью заряда и магнитной индукцией $\alpha = 30°$. Найдите силу Лоренца действующего на заряд.

$Дано:$
$q = 2\cdot 10^{-6}\ Кл$
$v = 8\ м/с$
$B = 0,25\ Тл$
$ \alpha = 30°$

$Найти: F = ?$

$Решение:$
На заряженное тело действует сила Лоренца, которая находится по формуле: $$F_Л = qvB sin \alpha = 2\cdot 10^{-6} \cdot 8 \cdot 0.25 \cdot \frac{1}{2} = 2 \cdot 10^{-6}\ Н$$

$Ответ: 2 \cdot 10^{-6}\ Н$

6.Электрон влетает в область однородного магнитного поля с индукцией $B = 1\ мкТл$ перпендикулярно линиям магнитной индукцией. Определите частоту вращения электрона.

$Дано:$
$q = 1,6\cdot 10^{-19}\ Кл$
$B = 1\ мкТл = 1 \cdot 10^{-6}\ Тл$
$ \alpha = 90°$
$m = 9.1 \cdot 10^{-31}\ кг$

$Найти: \nu = ?$

$Решение:$
На заряженное тело действует сила Лоренца, благодаря которой тело начнет двигаться по окружности с периодом: $$T = \frac{2 \pi m}{Bq}$$ Частота обратное значение периода, поэтому: $$\nu = \frac{1}{T} = \frac{Bq}{2 \pi m} = \frac{1 \cdot 10^{6} \cdot 1.6 \cdot 10^{-19}}{2 \cdot 3.14 \cdot 9.1 \cdot 10^{-31}} = 27997\ Гц \approx 28\ кГц$$

$Ответ: 28\ кГц$

7.Изобразите траекторию движения частиц

график

$Ответ:$ Находим по правилу левой руки:

а) электрон будет двигаться против часовой стрелки

б) протон будет двигаться против часовой стрелки

1. Вектор \(\vec{v}\) частицы параллелен к вектору магнитной индукции \(\vec{B}.\) В этом случае заряженная частица движется в магнитном поле вдоль линий магнитной индукции. Угол а между векторами \(\vec{v}\) и \(\vec{В}\) равен нулю или \(180°\). Так как в этом случае \(sin \alpha = 0\), то сила Лоренца тоже равна нулю. Магнитное поле на частицу не действует, и она движется равномерно и прямолинейно.
	2. Вектор \(\vec{v}\) частицы перпендикулярен \((\alpha = 90°)\) к вектору магнитной индукции \(\vec{B}\). В этом случае, поскольку сила Лоренца направлена перпендикулярно к скорости движения заряда, она создает частице центростремительное ускорение. Под действием силы Лоренца частица движется равномерно по окружности радиусом \(R\): $$R = \frac{mv}{qB}$$ Период вращения: $$T = \frac{2\pi m}{Bq}$$
	Вектор \(\vec{v}\) частицы направлен под некоторым углом \((\alpha \neq 90°)\) к вектору магнитной индукции \(\vec{B}\). Если заряженная частица влетает в магнитное поле под некоторым углом \(\alpha \neq 90°\), то она движется по винтовой траектории радиуса \(R\) и шагом \(h\)., развивающейся на линии напряженности поля. В случае движения отрицательной частицы направление вращательного движения будет противоположным.