Магнитное поле. Индукция магнитного поля.

Основные термины:

Магнит
магнитное поле
магнитная индукция
соленоид

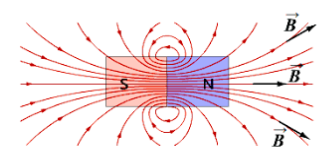
Постоянные магниты - это материалы, которые широко применяются в промышленности и быту. Для понимания их уникальных свойств важно понимать, как они устроены. Постоянные магниты создаются из сплавов железа, никеля и кобальта, которые обладают свойством "намагничиваться". Подобно положительным и отрицательным электрическим зарядам существуют северный и южный полюса магнита.

Вокруг магнитов существуют магнитные поля, посредством которых они взаимодействуют друг с другом и другими телами.
Силовые линии магнитного поля – это линии, касательные к которым совпадают с осью магнитной стрелки, помещенной в любую точку этого поля, а направление магнитного поля, созданного магнитом, принимают направление, которое указывает северный полюс магнитной стрелки. Тот конец магнита, из которого силовые линии выходят, является северным полюсом магнита. Противоположный конец, в который силовые линии входят,– южным полюсом магнита.

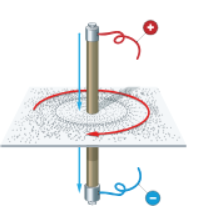
Между неподвижными электрическими зарядами действуют силы, определяемые законом Кулона. Между двумя проводниками, по которым течет ток, действуют силы, которые называются магнитными. Магнитное поле возникает в пространстве, окружающем электрические токи. Источник магнитного поля - движущийся заряд. Магнитное поле представляет собой особую форму материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Свойства магнитного поля:

порождается электрическим током;
обнаруживается по его действию на ток.

	Физическую величину, характеризующую силовое воздействие магнитного поля на проводник с током, называют магнитной индукцией $В$. Единица измерения магнитной индукции в СИ – $1\ Тесла\ [Тл].$ Французские физики Ж. Био и Ф. Савар в 1820 г. опытным путем установили величину магнитной индукции для прямого тока: $$B = \frac{\mu_0 \mu I}{2 \pi R}$$ $где\ B\ −\ магнитная\ индукция\ прямого\ проводника\ с\ током,\ силовая\ характеристика\ поля;$ $I\ −\ сила\ тока\ в\ проводнике;$ $R\ −\ кратчайшее\ расстояние\ от\ точки\ пространства\ до\ проводника;$ $ \mu_0 = 4\cdot 10^{-7}\ Н/А^2\ −\ магнитная\ постоянная;$ $\mu\ -\ магнитная\ проницаемость\ среды.$
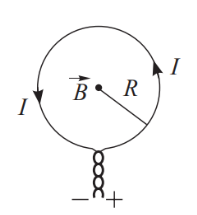
	Индукция магнитного поля в центре тонкого кругового витка, по которому течет ток, определяется соотношением: $$B = \frac{\mu_0 \mu I}{2 R}$$ $где\ B\ −\ магнитная\ индукция\ поля\ в\ центре\ кругового\ витка;$ $I\ −\ сила\ тока\ в\ проводнике;$ $R\ −радиус\ кругового\ витка.$
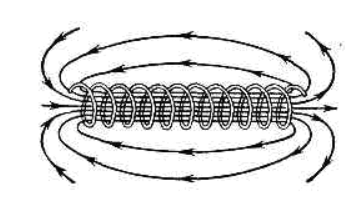
Соленоид - это катушка, у которой витки намотаны в одну сторону. Если длина соленоида гораздо больше радиуса его витков, то поле внутри соленоида можно считать однородным.
	Индукция магнитного поля внутри соленоида, по которому течет ток, определяется соотношением: $$B = \frac{\mu_0 \mu N I}{l} = \mu_0 \mu n I$$ $где\ B\ −\ магнитная\ индукция\ поля\ внутри\ соленоида;$ $N\ -\ число\ витков\ в\ соленоиде;$ $l\ -\ длина\ соленоида;$ $n = \frac{N}{l}\ число\ витков\ на\ единицу\ длины\ соленоида.$ Магнитное поле внутри соленоида однородно, силовые линии параллельны между собой.

Магнитную индукцию поля, созданного несколькими проводниками с током, определяют как векторную сумму магнитных индукций этих полей: $$\vec{B} = \vec{B_1} + \vec{B_2} + \dots + \vec{B_n}$$

Направление вектора магнитной индукции устанавливают с помощью правила “правого буравчика”. Если поступательное движение буравчика $v_n$ совместить с направлением тока в проводнике, то вращательное движение $v_{в}$ рукоятки укажет направление силовых линий магнитного поля.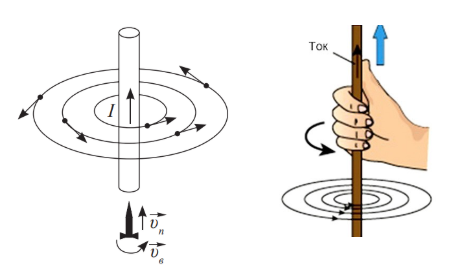

Направление магнитного поля катушки с током легко определить с помощью правила правой руки. Если правой рукой охватить катушку так, чтобы четыре пальца указывали направление тока в ее витках, то большой палец, отогнутый на $90°$, укажет направление магнитного поля. В отличие от силовых линий электрического поля силовые линии магнитного поля всегда замкнуты.
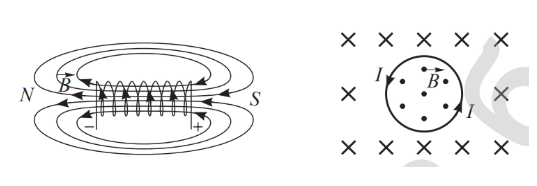
график

Примеры решения задач:

1.В прямом бесконечно длинном проводнике сила тока $I = 20\ А$. Определите магнитную индукцию в точке, удаленной на расстояние $R\ =\ 5\ см$ от проводника.

$Дано:$
$I = 20\ А$
$R\ =\ 5\ см =\ 5\cdot 10^{-2}\ м$

$Найти: B = ?$

$Решение:$
Магнитная индукция для прямого тока на расстоянии $R$ от провода в вакууме: $$B = \frac{\mu_0 \mu I}{2 \pi R} = \frac{4 \pi \cdot 10^{-7} \cdot 20}{2 \pi \cdot 5 \cdot 10^{-2}} = 80 \cdot 10^{-6}\ Тл = 80\ мкТл$$

$Ответ: 80\ мкТл$

2.Два длинных параллельных проводника находятся на расстоянии $d = 5\ см$ друг от друга. По проводникам в противоположных направлениях текут одинаковые токи $I = 10\ А$. Определите магнитную индукцию в точке, находящейся на расстоянии $2\ см$ от первого и $3\ см$ от второго проводника.

$Дано:$
$I = 10\ А$
$d\ =\ 5\ см =\ 5\cdot 10^{-2}\ м$
$R_1\ =\ 2\ см =\ 2\cdot 10^{-2}\ м$
$R_2\ =\ 3\ см =\ 3\cdot 10^{-2}\ м$

$Найти: B = ?$

$Решение:$
Магнитная индукция для прямого тока на расстоянии R от провода в вакууме находится по формуле: $$B = \frac{\mu_0 \mu I}{2 \pi R}$$ Точка находится между двумя проводами, поэтому одновременно через нее проходит два вектора магнитной индукции, значение которого найдется по их векторной сумме: $$\vec{B} = \vec{B_1} + \vec{B_2}$$ Нарисуем два провода с током в противоположных направлениях. По правилу буравчика определяем направление вектора магнитной индукции.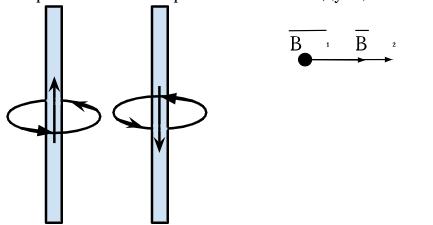
график

Получили одинаковое направление для векторов, их общее значение будет равна сумме длин векторов. $$B = B_1 + B_2 = \frac{\mu_0 \mu I}{2 \pi R_1} + \frac{\mu_0 \mu I}{2 \pi R_2} = \frac{\mu_0 \mu I}{2 \pi} (\frac{1}{R_1} + \frac{1}{R_2}) = $$ $$= \frac{4 \pi \cdot 10^{-7} \cdot 1 \cdot 10}{2 \pi} (\frac{1}{2 \cdot 10^{-2}} + \frac{1}{3 \cdot 10^{-2}}) \approx 1.67 \cdot 10^{-4}\ Тл$$

$Ответ: 1.67 \cdot 10^{-4}\ Тл$

3.В центре кругового тока радиусом $R = 5,8\ см$ индукция магнитного поля $B = 1.3 \cdot 10^{-4}\ Тл$. Определите силу тока.

$Дано:$
$B = 1.3 \cdot 10^{-4}\ Тл$
$R\ =\ 5.8\ см =\ 5.8\cdot 10^{-2}\ м$

$Найти: I = ?$

$Решение:$
Индукция магнитного поля в центре тонкого кругового витка, по которому течет ток, определяется соотношением: $$B = \frac{\mu_0 \mu I}{2 R}$$ Преобразуем формулу для нахождения силы тока: $$I = \frac{2 B R}{\mu_0 \mu} = \frac{2 \cdot 1.3 \cdot 10^{-4} \cdot 5.8\cdot 10^{-2}}{4\pi \cdot 10^{-7}} = 0.12\ А$$

$Ответ: 0.12\ А$

4.В каком направлении должен протекать ток в соленоиде, чтобы наблюдалось отталкивание соленоида от магнита?

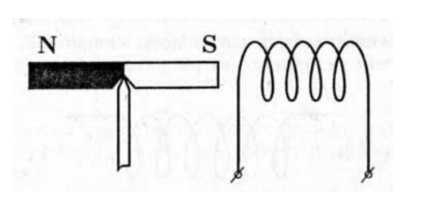
$Ответ:$
Чтобы соленоид отталкивался от магнита левый его конец должен быть южного полюса. Правый конец северного полюса. По правилу буравчика определяем, что для этого ток должен течь с правого конца в левый.

	Физическую величину, характеризующую силовое воздействие магнитного поля на проводник с током, называют магнитной индукцией \(В\). Единица измерения магнитной индукции в СИ – \(1\ Тесла\ [Тл].\) Французские физики Ж. Био и Ф. Савар в 1820 г. опытным путем установили величину магнитной индукции для прямого тока: $$B = \frac{\mu_0 \mu I}{2 \pi R}$$ \(где\ B\ −\ магнитная\ индукция\ прямого\ проводника\ с\ током,\ силовая\ характеристика\ поля;\) \(I\ −\ сила\ тока\ в\ проводнике;\) \(R\ −\ кратчайшее\ расстояние\ от\ точки\ пространства\ до\ проводника;\) \( \mu_0 = 4\cdot 10^{-7}\ Н/А^2\ −\ магнитная\ постоянная;\) \(\mu\ -\ магнитная\ проницаемость\ среды.\)
	Индукция магнитного поля в центре тонкого кругового витка, по которому течет ток, определяется соотношением: $$B = \frac{\mu_0 \mu I}{2 R}$$ \(где\ B\ −\ магнитная\ индукция\ поля\ в\ центре\ кругового\ витка;\) \(I\ −\ сила\ тока\ в\ проводнике;\) \(R\ −радиус\ кругового\ витка.\)
Соленоид - это катушка, у которой витки намотаны в одну сторону. Если длина соленоида гораздо больше радиуса его витков, то поле внутри соленоида можно считать однородным.
	Индукция магнитного поля внутри соленоида, по которому течет ток, определяется соотношением: $$B = \frac{\mu_0 \mu N I}{l} = \mu_0 \mu n I$$ \(где\ B\ −\ магнитная\ индукция\ поля\ внутри\ соленоида;\) \(N\ -\ число\ витков\ в\ соленоиде;\) \(l\ -\ длина\ соленоида;\) \(n = \frac{N}{l}\ число\ витков\ на\ единицу\ длины\ соленоида.\) Магнитное поле внутри соленоида однородно, силовые линии параллельны между собой.