Излучение. Фотоны. Квантовые гипотезы

Излучение — передача энергии в форме волн или частиц через пространство или материальную среду. Основные виды: Электромагнитное излучение — радиоволны, микроволны, инфракрасное, видимый свет, ультрафиолет, рентгеновское и гамма-излучение. Излучение частиц — альфа (α), бета (β), нейтронное и нейтринное. Акустическое излучение — ультразвуковые, звуковые и сейсмические волны. Гравитационное излучение — рябь кривизны пространства-времени.

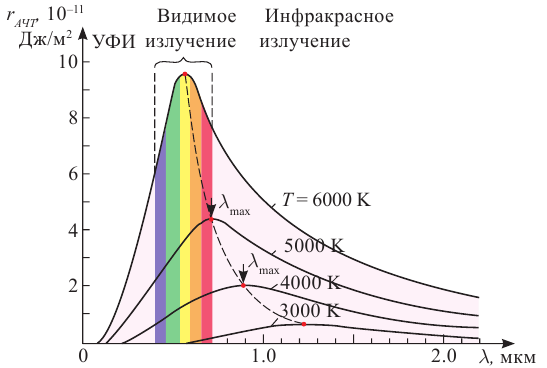
Тепловое излучение — электромагнитное излучение нагретых тел за счёт их внутренней энергии.

• Темные поверхности излучают и поглощают лучше, чем светлые.
• Абсолютно черное тело — идеальное тело, полностью поглощающее и излучающее во всём спектре.

Закон Стефана–Больцмана:

$$ R = \sigma T^4 $$

где:

• \( R \) — энергия излучения с 1 м² поверхности за 1 с,
• \( \sigma = 5.67 \cdot 10^{-8} \ \text{Вт/м}^2 \text{K}^4 \) — постоянная Стефана–Больцмана,
• \( T \) — температура в К.

Гипотеза Планка:
Атомы излучают энергию отдельными порциями — квантами.

$$ E = h \nu $$

где:

• \( E \) — энергия кванта,
• \( h = 6.626 \cdot 10^{-34} \ \text{Дж·с} \) — постоянная Планка,
• \( \nu \) — частота излучения.

Фотон — квант электромагнитного излучения.

Основные свойства фотона:

• частица электромагнитного поля,
• движется со скоростью света,
• не имеет массы покоя,
• существует только в движении.

Энергия фотона:
$$ E = h \nu $$

Импульс фотона:
$$ p = \frac{h}{\lambda} $$

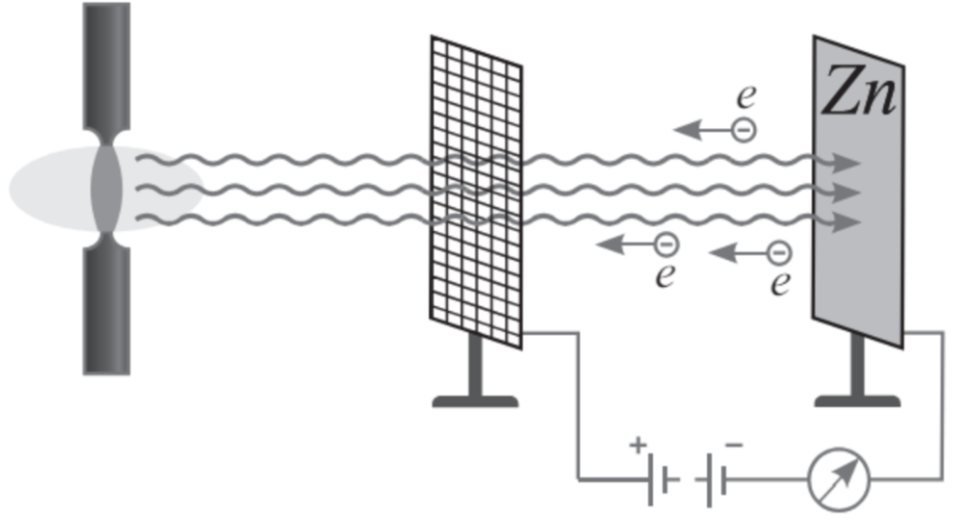
Фотоэффект — вырывание электронов из вещества под действием света. Законы, установленные опытами Столетова: Электроны вылетают с поверхности металла под действием света. Фотоэффект возникает только при облучении высокочастотным светом. Скорость фотоэлектронов растет с увеличением частоты. Число электронов пропорционально интенсивности света.

Уравнение Эйнштейна для фотоэффекта:

$$ h \nu = A_\text{вых} + \frac{mv^2}{2} $$

где:

• \( A_\text{вых} \) — работа выхода,
• \( \frac{mv^2}{2} \) — кинетическая энергия электрона.

Красная граница фотоэффекта:

$$ \nu_\text{min} = \frac{A_\text{вых}}{h}, \qquad \lambda_\text{max} = \frac{hc}{A_\text{вых}} $$

Виды фотоэффекта:

• Внешний фотоэффект — испускание электронов с поверхности металла.
• Внутренний фотоэффект — изменение проводимости вещества под действием света.

Давление света

Свет оказывает давление благодаря наличию импульса у фотонов.

Для падающего пучка:

$$ p = \frac{I}{c} (1 + \rho) $$

где:

• \( p \) — давление,
• \( I \) — интенсивность света,
• \( \rho \) — коэффициент отражения (для зеркала \( \rho = 1 \), для черного тела \( \rho = 0 \)).

Корпускулярно-волновой дуализм

Свет обладает двойственной природой:

• как волна: интерференция, дифракция, поляризация,
• как частица: фотоэффект, давление света.

Принцип дополнительности (Н. Бор): только совместное рассмотрение корпускулярных и волновых свойств даёт полное описание света.

Гипотеза де Бройля
Каждой частице с импульсом \( p \) соответствует волна длиной:

$$ \lambda_\text{Бр} = \frac{h}{p} = \frac{h}{mv} $$

Примеры решения задач

1. Определите мощность излучения единичной площади поверхности Солнца. Температура поверхности равна \( T = 6000 K \).

2. Во сколько раз излучение металла при \( 2000 K \) больше, чем при \( 727^\circ C \)?

3. Фотон выбивает с поверхности металла электрон, если работа выхода \( W = 2эВ \). Кинетическая энергия фотоэлектрона равна \( K = 2эВ \). Определить минимальную энергию фотона.