lessons.kz
Физика ЕНТ
Кинематика
Ускорение свободного падения. Движение по вертикали.

Ускорение свободного падения. Движение по вертикали.

Основные термины:

Свободное падение
Ускорение свободного падения

Свободное падение – это движение тел в безвоздушном пространстве под действием силы тяжести. Обычно так происходит, если пренебречь силами сопротивления. Поэтому все тела независимо от массы падают в вакууме с одинаковым ускорением. При этом ускорение тела будет постоянным как по направлению, так и по величине: $a = g = 9.8 м/с^2$ . Его называют ускорением свободного падения. Оно направлено вниз перпендикулярно поверхности (к центру Земли).

Движение тела при свободном падении.

Свободное падение тела является примером прямолинейного равнопеременного движения, следовательно, все формулы, изученные ранее, справедливы и для этого вида движения. Отличие формул заключается в том, что перемещение по вертикали принято называть высотой и обозначать буквой $h$. При движении по вертикали ось координат, как правило, обозначают $Oy$ и, соответственно, вводят координату $y$.

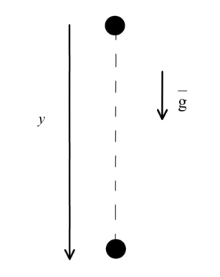	Уравнение скорости: $$\vec{v} = \vec{v_0} + \vec{g} \cdot t$$ Уравнение перемещения :$$\vec{h} = \vec{v_{0y}} t + \frac{\vec{g_y} t^2}{2} $$		В проекции на ось у: $$v_y = v_{0y} + g_yt $$ Уравнение перемещения в проекции на ось у:$$h = v_{0y} t + \frac{g_y t^2}{2} $$
	Уравнение координаты: $y=y_0+v_{0y}t+ \frac{g_yt^2}{2}$

Закон, по которому определяется перемещение тела при свободном падении без начальной скорости: $h = \frac{gt^2}{2}$. Ну а время падения тогда будет определятся по формуле: $t_{падения} = \sqrt{\frac{2h}{g}}$. Зная время падения можно найти скорость в момент столкновения: $v=g\cdot t_{падения}=\sqrt{2gh}$.

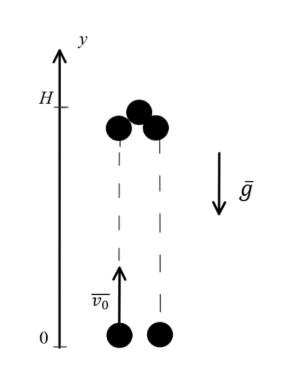
Движение тела подброшенного вверх с начальной скоростью.

Пусть тело брошено вертикально вверх с начальной скоростью $v_0$. Тело движется вверх с убывающей скоростью, останавливается, затем движется вниз равноускорено. Если направить координатную ось $Oу$ вверх, то проекция ускорения будет отрицательной.

Формулы расчета скорости и перемещения в модулях примут вид:
$v_y = v_{0y} - g_yt $ $h = v_{0y} t - \frac{g_y t^2}{2} $
Закон движения в этом случае запишется в виде: $y=y_0+v_{0y}t - \frac{g_yt^2}{2}$
Тело достигает максимальной высоты при скорости равной нулю. Это время подъема можно определить, записав уравнение скорости для тела и приняв конечную скорость, равной нулю:
$v=v_0-gt \quad \quad \Rightarrow \quad \quad 0 = v_0 - gt \quad \quad \Rightarrow \quad \quad t_{под} = v_0 g$
Зная время подъема определяем максимальную высоту достигаемую телом: $H = v_0t_{под} - \frac{gt_{под}^2}{2} = \frac{v_0^2}{g} - \frac{v_0^2}{2g} = \frac{v_0^2}{2g}$
При подбрасывании тела вверх с поверхности земли движение тела является равнозамедленным для первой половины и равноускоренным для второй половины движения. Так как модуль ускорения постоянен мы получим равность времени подъема и падения. $t_{полное} = 2 \cdot t_{под}$

Примеры решения задач:

1. Тело свободно падает с высоты $5\ м$ без начальной скорости. С какой скоростью тело достигнет поверхности Земли? Принять $g = 10\ м/с^2$

$Дано:$
$h = 5\ м$
$g = 10\ м/с^2$

Найти: $v = ?$

$Решение:$
Закон движения тела подброшенного вверх: $v = gt$
Для того чтобы определить время падения преобразуем уравнение перемещения $h = \frac{gt^2}{2}$ и получим следующую формулу: $t = \sqrt{\frac{2h}{g}}$
Подставив в формулу скорости: $v = gt = \sqrt{2gh}$ $$v = \sqrt{2gh} = \sqrt{2 \cdot 10\ м/с^2 \cdot 5\ м} = 10\ м/с$$

$Ответ: v = 10\ м/с$

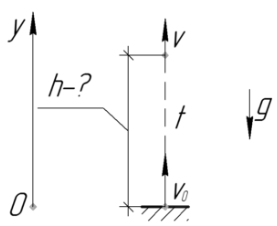
2. Тело брошено со скоростью $40\ м/с$. Определить высоту подъема тела через $2 с$.

$Дано:$ $v = 40\ м/с$ $g = 10\ м/с^2$ $t = 2\ с$	$Решение:$
		Давайте запишем уравнение движения тела вдоль введенной нами оси y. Начальная координата равна нулю, вектор ускорения свободного падения направлен в обратную сторону оси, поэтому проекция на ось будет отрицательного характера: $y=v_{0y}t- \frac{g_yt^2}{2}$. Так как мы ввели начало оси у земли, то координата тела на 2 с будет являться искомой высотой: $h=v_{0y}t- \frac{g_yt^2}{2}$ $$h=v_{0y}t- \frac{g_yt^2}{2} = h=40\ м \cdot 2\ с- \frac{10\cdot 2^2}{2} = 60\ м$$ $Ответ: h = 60\ м$

3. Тело брошено вертикально вверх со скоростью 50 м/с. Через какое время оно упадет на Землю?

$Дано:$
$v = 50\ м/с$
$g = 10\ м/с^2$

Найти: $t = ?$

$Решение:$
Движение тела является равноускоренным без начальной скорости. $y=y_0+v_{0y}t -\frac{g_yt^2}{2}$
Пусть начальная координата оси будет совпадать с землей. Тогда $y_0=0$. И также в момент падения $t$ тело будем иметь координату $y = 0$. Подставив в закон движения получим следующее уравнение:
$0 = v_0t - \frac{g_yt^2}{2} \quad \quad $
Вынесем за скобку общий множитель $t$ : $0 = (v_0 - \frac{g_yt}{2}) t \quad \quad \Rightarrow \quad \quad t = 0; \quad \quad v_0 - \frac{g_yt}{2} = 0$
$t = 0$ это момент начала движения и в нем действительно координата равна нулю. Но нам нужно следующее значение времени. Для этого преобразуем второе уравнение.
$v_0 - \frac{g_yt}{2} = 0 \quad \quad \Rightarrow \quad \quad v_0 = \frac{gt}{2} \quad \quad \Rightarrow \quad \quad t =\frac{2v_0}{g}=\frac{2 \cdot 50\ м/с}{10\ м/c^2} = 10\ с$

$Ответ: t = 10\ с$

	Уравнение скорости: $$\vec{v} = \vec{v_0} + \vec{g} \cdot t$$ Уравнение перемещения :$$\vec{h} = \vec{v_{0y}} t + \frac{\vec{g_y} t^2}{2} $$		В проекции на ось у: $$v_y = v_{0y} + g_yt $$ Уравнение перемещения в проекции на ось у:$$h = v_{0y} t + \frac{g_y t^2}{2} $$
	Уравнение координаты: \(y=y_0+v_{0y}t+ \frac{g_yt^2}{2}\)

\(Дано:\) \(v = 40\ м/с\) \(g = 10\ м/с^2\) \(t = 2\ с\)	\(Решение:\)
		Давайте запишем уравнение движения тела вдоль введенной нами оси y. Начальная координата равна нулю, вектор ускорения свободного падения направлен в обратную сторону оси, поэтому проекция на ось будет отрицательного характера: \(y=v_{0y}t- \frac{g_yt^2}{2}\). Так как мы ввели начало оси у земли, то координата тела на 2 с будет являться искомой высотой: \(h=v_{0y}t- \frac{g_yt^2}{2}\) $$h=v_{0y}t- \frac{g_yt^2}{2} = h=40\ м \cdot 2\ с- \frac{10\cdot 2^2}{2} = 60\ м$$ \(Ответ: h = 60\ м\)