lessons.kz
Физика ЕНТ
Кинематика
Прямолинейное равнопеременное движение. Ускорение. Уравнение движения и скорости.

Прямолинейное равнопеременное движение. Ускорение. Уравнение движения и скорости.

Основные термины:

ускорение
равноускоренное движение
уравнение скорости
равнозамедленное движение
уравнение скорости
уравнение движения

Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.

Ускорение - физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло. $$ \vec{a} = \frac{\vec{v}\ - \vec{v_0}}{t}$$

Вектор скорости при равнопеременном движении определяется благодаря следующему уравнению: $ \vec{v} = \vec{v_0} + \vec{a} \cdot t$
аналогичной будет формула в проекциях: $v_x = v_{0x} + a_x t$

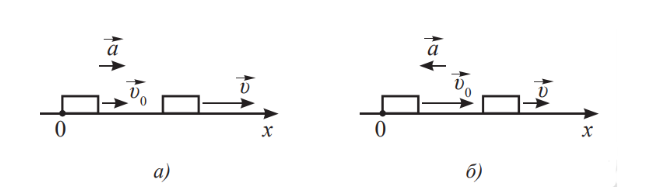
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает. При равноускоренном движении (РУД) проекции векторов $v_{0x},\ v_x,\ a_x$ положительные (рис. а). Формула расчета скорости через модули векторов примет вид: $v = v_0 + at$
Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается. Для равнозамедленного движения (РЗД, рис. б) проекция ускорения – отрицательная, следовательно, формула расчета скорости примет вид: $v = v_0 - at$

Запись расчета перемещения при равноускоренном движении выглядит следующим образом: $s = v_0 t + \frac{a t^2}{2}$
Для равнозамедленного: $s = v_0 t - \frac{a t^2}{2}$

Закон уравнения движения при равнопеременном движении: $x = x_0 + v_{0x}t + \frac{a_x t^2}{2}$

Примеры решения задач

1. Самолет проходит взлетную полосу за $10\ с$, в момент отрыва от земли его скорость равна $100\ м/с$. Какой путь проедет самолет за это время?

$Дано:$
$v = 100\ м/с$
$t = 10\ с$

$Найти: s = ?$

$Решение:$
Самолет движется равноускорено без начальной скорости. Поэтому уравнение перемещения будет выглядеть: $s = \frac{a\ t^2}{2}$
Но для расчета перемещения нам не хватает значение ускорения. Благодаря тому что мы знаем значение скорости в момент отрыва, можем подсчитать ускорение по следующей формуле: $$a = \frac{v - v_0}{t} = \frac{v}{t} = \frac{100\ м/с}{10\ c} = 10\ м/с^2$$ $$s = \frac{a\ t^2}{2} = \frac{10\ м/с^2 \cdot 10^2\ с^2}{2} = 500\ м$$
$Ответ: s =500\ м$

2. Поезд при скорости $54\ км/ч$ начал тормозить с ускорением $0,6\ м/с^2$. Найти время торможения.

$Дано:$
$v_0 = 54\ км/ч = 15\ м/с$
$a = 0.6\ м/с^2$

$Найти: t = ?$

$Решение:$
Движение является равнозамедленным, так как скорость тела снижается с каждой секундой пока не достигнет нуля. Поэтому уравнение скорости будет выглядеть: $v = v_0 - at$ , преобразуем формулу для подсчета времени: $t = \frac{v_0 - v}{a}$
Торможение это отсутствие движение, поэтому $v = 0\ м/с$.
Подставляем значения. $$ t = \frac{v_0 - v}{a} = \frac{(15\ -\ 0)\ м/с}{0.6\ м/с^2} = 25\ с$$
$Ответ: t =25\ с$

3. За какое время автомобиль, двигаясь из состояния покоя ускорением $60\ см/с^2$, пройдет путь $30\ м$?

$Дано:$
$a = 60\ см/с^2 = 0.6\ м/с^2$
$s = 30\ м$

$Найти: t = ?$

$Решение:$
Автомобиль движется равноускорено без начальной скорости. Поэтому уравнение перемещения будет выглядеть: $s = \frac{at^2}{2}$
преобразуем формулу для подсчета времени: $$ t = \sqrt{\frac{2s}{a}} = \sqrt{\frac{2 \cdot 30\ м}{0.6\ м/с^2}} = 10\ с $$
$Ответ: t = 10\ с$

4. Движения четырех материальных точек заданы следующими уравнениями (соответственно): $x_1 = 10t + 0.4t^2; \ x_2 = 2t - t^2;\ x_3 = -4t + 2t^2;\ x_4 = -t - 6t^2$
Выполните задания: а) напишите уравнение $v = v(t)$ для каждой точки; б) опишите движение каждой точки.

Решение: а) Общий вид уравнения скорости выглядит следующим образом:$v = v_0 + a_xt$. И для ее построения нам необходимо знать начальную скорость $v_0$ и ускорение тела $a$. Для получения этих данных используем уравнение движения тел, который имеет общий вид $x = x_0 + v_{0x}t + \frac{a_xt^2}{2}$.
То есть пустой коэффициент это $x_0$, коэффициент перед первой степенью $t$ это начальная скорость $v_{0x}$ и коэффициент перед квадратом $t$ это поделенное на два ускорение $a_x$.

б) Благодаря знаку начальной скорости определяем направление движения. Если оно положительно, то по движение происходит по оси $Ox$. Если оно отрицательно, то против оси $Ox$. По значению ускорения определяем является ли движение равнозамедленным или равноускоренным.

$x_1 = 10t + 0.4t^2$	$v_{0x} = 10$ $\frac{a_x}{2} = 0.4$ $a_x = 2\cdot 0.4 = 0.8 $	$v = 10 + 0.8t$	равноускоренное по направлению оси
$x_2 = 2t - t^2$	$v_{0x} = 2$ $\frac{a_x}{2} = -1$ $a_x = 2\cdot (-1) = -2 $	$v = 2 - 2t$	равнозамедленное по направлению оси
$x_3 = -4t + 2t^2$	$v_{0x} = -4$ $\frac{a_x}{2} = 2$ $a_x = 2\cdot 2 = 4 $	$v = -4 + 4t$	равноускоренное в противоположном направлении
$x_4 = -t - 6t^2$	$v_{0x} = -1$ $\frac{a_x}{2} = -6$ $a_x = 2\cdot (-6) = -12 $	$v = -1 - 12t$	равнозамедленное в противоположном направлении

\(x_1 = 10t + 0.4t^2\)	\(v_{0x} = 10\) \(\frac{a_x}{2} = 0.4\) \(a_x = 2\cdot 0.4 = 0.8 \)	\(v = 10 + 0.8t\)	равноускоренное по направлению оси
\(x_2 = 2t - t^2\)	\(v_{0x} = 2\) \(\frac{a_x}{2} = -1\) \(a_x = 2\cdot (-1) = -2 \)	\(v = 2 - 2t\)	равнозамедленное по направлению оси
\(x_3 = -4t + 2t^2\)	\(v_{0x} = -4\) \(\frac{a_x}{2} = 2\) \(a_x = 2\cdot 2 = 4 \)	\(v = -4 + 4t\)	равноускоренное в противоположном направлении
\(x_4 = -t - 6t^2\)	\(v_{0x} = -1\) \(\frac{a_x}{2} = -6\) \(a_x = 2\cdot (-6) = -12 \)	\(v = -1 - 12t\)	равнозамедленное в противоположном направлении