Механическое движение. Прямолинейное равномерное движение.

Основные термины:

• Механическое движение
• Материальная точка
• Система отсчета
• Траектория
• Перемещение
• Путь
• Равномерное движение
• Скорость
• Мгновенная скорость
• Средняя скорость
• Закон сложения скоростей
• Уравнение движения

Механическое движение — это изменение положения тела в пространстве, относительно других тел с течением времени. По характеру движения точек различают три вида движения: a) поступательное — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе; б) вращательное движение, при котором все точки тела движутся по окружностям; в) колебательное движение — движение, которое повторяется или почти повторяется. По виду траектории различают прямолинейное и криволинейное движения (частный случай криволинейного движения - движение по окружности); по скорости - равномерное и неравномерное; по ускорению - равноускоренное, равнозамедленное, ускоренное.

Основная задача механики — определять положение тела в пространстве в любой момент времени.

Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи. Тело можно принять за материальную точку, если оно движется поступательно или если его размеры много меньше расстояний, которые тело проходит. Систему отсчета вводят для того, чтобы задать положение материальной точки в пространстве. В нее входят: тело отсчета (любое тело), система координат (одномерная, двухмерная или трехмерная) и часы (начало отсчета времени совпадает с началом движения тела).

Траектория - линия, вдоль которой движется тело.

Путь \(l (м)\) - длина траектории.

Перемещение \(s (м)\) - это вектор, соединяющий начальное положение тела с конечным. Обычно \(l>s\) . Если тело движется по прямой \(l=s\)

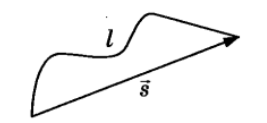
Проекции вектора перемещения на оси координат

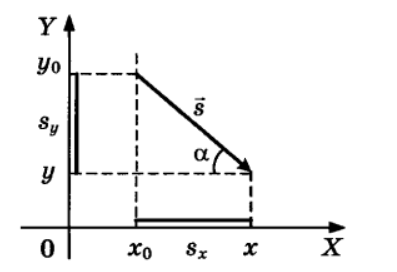
Проекция вектора перемещения на ось \(OX\): \(s_x=x-x_0\) Проекция вектора перемещения на ось \(OY\): \(s_y=y-y_0\) Проекция вектора на ось равна нулю, если вектор перпендикулярен оси. Знаки проекций перемещения: проекцию считают положительной, если движение от проекции начала вектора к проекции конца происходит по направлению оси, и отрицательной, если против оси. В данном примере \(s_x>0; \quad s_y<0\) Модуль перемещения - это длина вектора перемещения: \(|\vec{s}|=s\) По теореме Пифагора: \(s=\sqrt{s^2_x+s^2_y}\)   или   \(s=\sqrt{(x-x_0)^2+(y-y_0)^2}\) Проекция перемещения и угол наклона  \(s_x=\pm s \cos \alpha; \quad \quad s_y=\pm s \sin \alpha\)

Равномерное прямолинейное движение

Равномерное прямолинейное движение - движение, при котором тело за любые равные промежутки времени, совершает равные перемещения.

Скорость \(v (м/с)\) — векторная физическая величина, которая показывает, какое перемещение совершает тело за единицу времени. В векторном виде:   \(\vec{v}=\frac{\vec{s}}{t}\)
В проекциях на ось OX:   \(v_x=\frac{s_x}{t}=\frac{\Delta x}{\Delta t}\)
Измерительный прибор - спидометр - показывает модуль скорости.
Знак проекции скорости зависит от направления вектора скорости и оси координат:

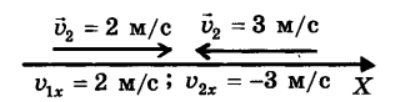
График координаты - зависимость координаты тела от времени:   \(x=x_0+v_xt \)

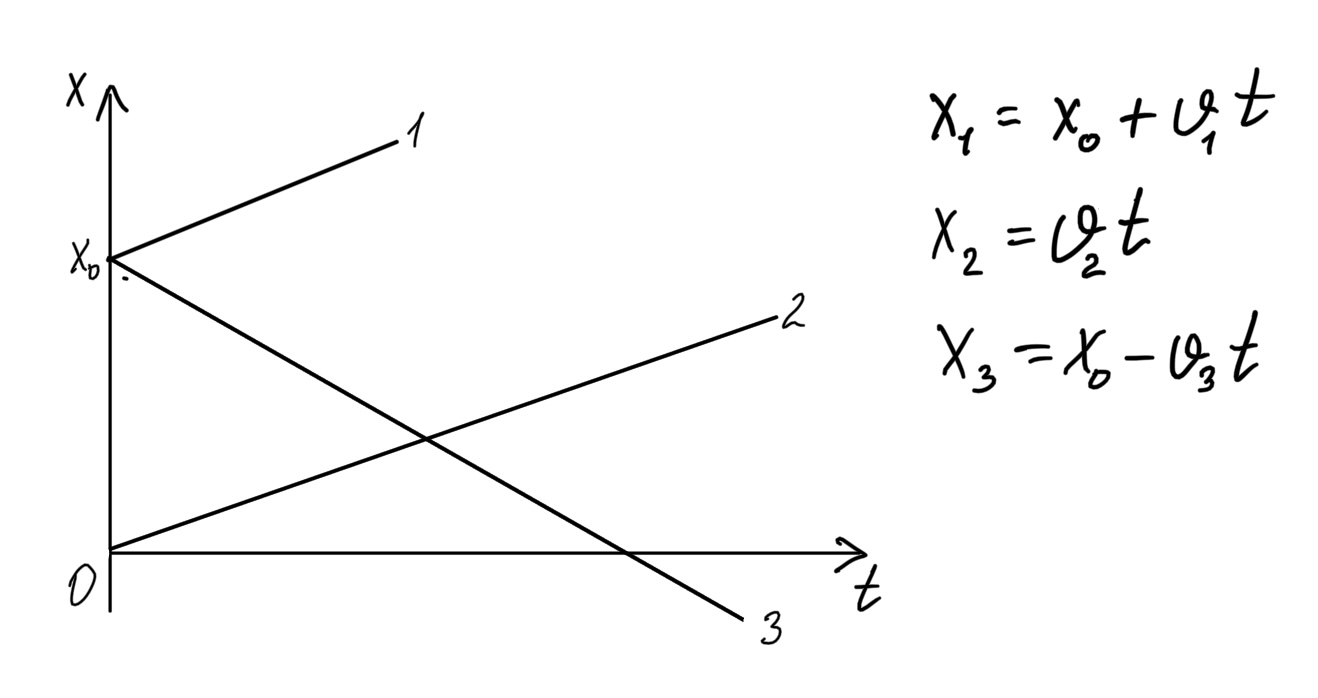
Относительность механического движения.

Под относительностью механического движения мы понимаем зависимость чего-либо от выбора системы отсчета. Например покой относителен, движение относительно и положения тела относительно.

Правило сложения скоростей. Векторная сумма скоростей:   $$\vec{v’} = \vec{v}+\vec{u}$$
где   \(\vec{v}\) - скорость тела относительно подвижной системы отсчета (ПСО),
\(\vec{u}\) - скорость ПСО относительно неподвижной системы отсчета (НСО),
\(\vec{v’}\)- скорость тела относительно неподвижной системы отсчета (НСО).

Неравномерное движение

Неравномерное движение - движение с переменной скоростью. Является самой распространенным видом движения.

Средняя скорость:   $$v_{ср}=\frac{s}{t}=\frac{s_1+s_2+...+s_n}{t_1+t_2+...t_n}$$
\(s\) - весь путь,   \(t\) - все время.

Примеры решения задач

1. Автобус из Алматы до Сарыозека прошел 180 км за 2,5 ч. Считая движение автобуса равномерным, нужно найти его скорость в Международной системе единиц.

2. Автомобиль первые 40 мин двигался со скоростью 60 км/ч, следующие 20 мин – со скоростью 30 км/ч. Какова средняя скорость автомобиля в м/с?

3. Автоколонна длиной 2 км движется со скоростью 40 км/ч. Мотоциклист выехал из хвоста колонны со скоростью 60 км/ч. За какое время он достигнет головной машины?