Движение тела брошенного горизонтально. Движение тела подброшенного под углом к горизонту.

Основные термины:

• проекция вектора
• ускорение свободного падения

Движение тела брошенного горизонтально.

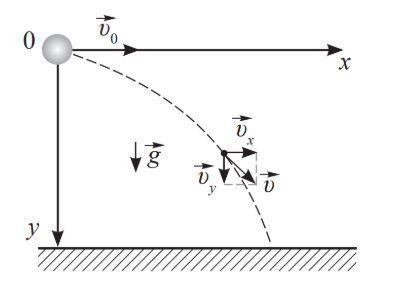
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: \(Ox\) и \(Oy\).

Вектор скорости горизонтально брошенного тела направлен по касательной траектории его движения. Она будет иметь две проекции, благодаря сумме которых можно получить сам вектор скорости. \( \vec{v_x} \) - геометрическая проекция скорости на ось \( Ox \) , \( \vec{v_y} \) - геометрическая проекция скорости на ось \(Oy \). $$\vec{v}\ =\ \vec{v_x}\ +\vec{v_y}$$ Модуль мгновенной скорости в момент времени \(t\) можно вычислить по теореме Пифагора: $$ |v| = \sqrt{v_x^2\ +\ v_y^2}$$

Рассмотрим движение тела на каждой оси по отдельности.

Так как вектор ускорения перпендикулярен оси \(Ox\) , его проекция будет равна нулю. Движение будет равномерным. \(v_x\ =\ const.\)   Вектор начальной скорости направлен горизонтально, значит проекция начальной скорости на ось \(Ox\) будет совпадать с самим вектором: $$v_{0x}\ =\ v_0 $$ $$v_x\ =\ v_{0x}\ =\ v_0\ =\ const.$$ $$x\ =\ x_0\ +\ v_xt$$ $$s\ =\ v_xt$$

Вектор начальной скорости направлен горизонтально, значит проекция начальной скорости на оси \(Oy\) будет равен нулю: $$v_{0y}\ =\ 0 $$ $$v_y\ =\ gt $$ $$y\ =\ y_0\ +\ \frac{gt^2}{2}$$ $$h\ =\ \frac{gt^2}{2}$$ Если \(h\) - это высота броска тела, то время на падение будет рассчитано по следующей формуле \(t_{падения}\ =\ \sqrt{\frac{2h}{g}}\) Зная время падения можно найти скорость тела по оси \(y\) в момент столкновения: \(v_y\ =\ gt_{падения}\ =\ \sqrt{2gh}\).

Движение тела подброшенного под углом к горизонту.

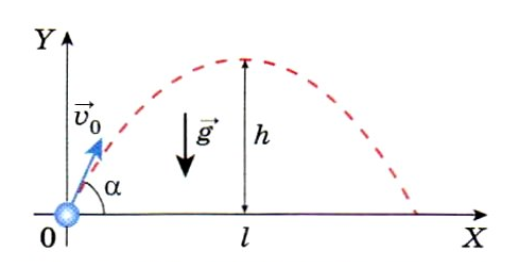
	Тело, брошенное под некоторым углом к горизонту, свободно падает, так как движется под действием только силы тяжести.
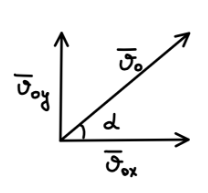
		Вектор начальной скорости \( \vec{v_0} \) подброшенного под углом тела будет иметь угол \(\alpha\) с осью \(Ox\), значит и со своей проекцией на ось \(x\ \vec{v_{0x}}\). Скалярная проекция вектора на оси вычисляется по формуле: $$v_{0x}\ =\ v_0 \cdot \cos\alpha$$ $$v_{0y}\ =\ v_0 \cdot \sin\alpha$$

Знак определяется в зависимости от направления оси. Данные формулы были получены благодаря соотношениям в прямоугольном треугольнике:
$$ \cos\alpha\ =\ \frac{прилежащий\ катет}{гипотенуза}\ =\ \frac{|\vec{v_{0x}}|}{|\vec{v_0}|} \quad \quad \quad \quad \sin\alpha\ =\ \frac{противолежащий\ катет}{гипотенуза}\ =\ \frac{|\vec{v_{0y}}|}{|\vec{v_0}|}$$

Передвижение по оси \(\textbf{Ox}\) будет равномерным с постоянной скоростью: $$v_{0x}\ =\ v_0 \cdot \cos\alpha$$ $$v_x\ =\ v_{0x}\ =\ v_0 \cdot\cos\alpha =\ const.$$ $$x\ =\ x_0\ +\ v_xt\ =\ x_0\ +\ v_0\cos\alpha\cdot t$$ $$s\ =\ v_xt\ =\ v_0\cos\alpha\cdot t$$

Передвижение по оси \(\textbf{0y}\) будет иметь характеристику равнопеременного движения с постоянным по модулю ускорением равным \(g\ =\ 10\ м/с^2\). Формулы расчета скорости, перемещения и координаты вдоль оси \(Оу\) определяют по формулам подброшенного тела с использованием составляющей начальной скорости по указанной оси. $$v_{0y}\ =\ v_0\cos\alpha$$ $$v_y\ =\ v_{0y}\ -\ gt\ =\ v_0\sin\alpha\ -\ gt$$ $$h\ =\ v_{0y}t\ -\ \frac{gt^2}{2}\ =\ v_0\sin\alpha t\ - \ \frac{gt^2}{2}$$ $$y\ =\ y_0\ +\ v_0\sin\alpha t\ - \ \frac{gt^2}{2}$$ Обозначим максимальную высоту подъёма тела как \(H\), а момент времени, в который тело достигло наибольшей высоты, через \(t_{под.}\). Тело движется вверх с уменьшением скорости по вертикальной оси и в наивысшей точке траектории \(v_y\ =\ 0\), то $$v_y\ =\ v_{0y}\ -\ gt \quad \quad \Rightarrow \quad \quad 0\ =\ v_{0y}\ -\ gt_{под} \quad \quad \Rightarrow \quad \quad t_{под}\ =\ \frac{v_{0y}}{g}\ =\ \frac{v_0 \sin\alpha}{g}$$ Подставив полученное время в уравнение движения по оси \(y\) мы получим: $$H\ =\ v_{0y}t\ -\ \frac{gt_{под}^2}{2}\ =\ v_{0}\sin\alpha \cdot \frac{v_0 \sin\alpha}{g}\ -\ \frac{g\cdot(\frac{v_0 \sin\alpha}{g})^2}{2}\ =\ \frac{v_0\sin\alpha}{g}\ -\ \frac{v_0\sin\alpha}{2g}\ =\ \frac{v_0\sin\alpha}{2g}$$

Примеры решения задач:

1. Дальность полета тела, брошенного горизонтально со скоростью \(4,9\ м/с\), равна высоте, с которой его бросили. Чему равна эта высота?

\(Дано:\) \(v_0 = 4.9\ м/с\) \(g = 9.8\ м/с^2\) \(l\ =\ h\) \(Найти: h = ?\)

\(Решение:\) Построим уравнения движения тела по обеим координатным осям. $$l\ =\ v_xt_{пад} \quad \quad \quad h\ =\ \frac{gt_{пад}^2}{2}$$ Движение по оси \(Ох\) равномерное и тело было брошено горизонтально (по оси \(Ох\)), поэтому \(v_x\ =\ v_{0x}\ =\ v_0\) По дано задачи \(l\ =\ h\), подставив вместо них выражения в зависимости от времени падения получим уравнение зависимое от времени падения, решив которое получим его. $$v_0t\ =\ \frac{gt_{пад}^2}{2} \quad \quad \Rightarrow \quad \quad 2v_0\ =\ gt \quad \quad \Rightarrow \quad \quad t\ =\ \frac{2v_0}{g}\ $$ Подставим в формулу \(l\) или \(h\) $$h\ =\ \frac{gt^2}{2}\ =\ \frac{g\cdot(2v_0\ /\ g)^2}{2}\ =\ \frac{2v_0^2}{g}\ =\ \frac{2\cdot4.9\ м/с}{9.8\ м/с^2}\ =\ 4.9\ м $$ \(Ответ: h = 4.9\ м\)

2. Мяч брошен с начальной скоростью \(200\ дм/с\) под углом \(30°\) к горизонту. Чему равна максимальная высота подъема мяча?

\(Дано:\) \(v_0 = 200\ дм/с\ =\ 20\ м/с\) \(g = 10\ м/с^2\) \(\alpha\ =\ 30°\) \(Найти: h = ?\)

\(Решение:\) Построим уравнения движения тела по обеим координатным осям. $$l\ =\ v_xt_{пад} \quad \quad \quad h\ =\ \frac{gt_{пад}^2}{2}$$ Движение по оси \(Ох\) равномерное и тело было брошено горизонтально (по оси \(Ох\)), поэтому \(v_x\ =\ v_{0x}\ =\ v_0\) По дано задачи \(l\ =\ h\), подставив вместо них выражения в зависимости от времени падения получим уравнение зависимое от времени падения, решив которое получим его. $$v_0t\ =\ \frac{gt_{пад}^2}{2} \quad \quad \Rightarrow \quad \quad 2v_0\ =\ gt \quad \quad \Rightarrow \quad \quad t\ =\ \frac{2v_0}{g}\ $$ Подставим в формулу \(l\) или \(h\) $$h\ =\ \frac{gt^2}{2}\ =\ \frac{g\cdot(2v_0\ /\ g)^2}{2}\ =\ \frac{2v_0^2}{g}\ =\ \frac{2\cdot4.9\ м/с}{9.8\ м/с^2}\ =\ 4.9\ м $$ \(Ответ: h = 4.9\ м\)

3. Пуля вылетает из ствола под углом \(45°\) к горизонту со скоростью \(60\ м/с\). На каком ближайшем расстоянии, считая по горизонтальному направлению от места выстрела, будет находиться пуля на высоте \(50\ м\)?

\(Дано:\) \(v_0 = 60\ м/с\) \(g = 10\ м/с^2\) \(\alpha\ =\ 45°\) \(h\ =\ 50\ м\) \(Найти: s = ?\)

\(Решение:\) Тело было подброшено под углом к горизонту. Для начала найдем время в котором тело будет находится на заданной высоте, подставив в уравнение высоты \(50\ м\). \(h\ =\ v_{0y}t\ -\ \frac{gt^2}{2}\ =\ v_{0}\sin\alpha t\ -\ \frac{gt^2}{2}\) \(50\ м\ =\ 60\cdot\sin45°\ -\ \frac{10\cdot t^2}{2}\) \(50\ =\ 30\sqrt{2}t\ -\ 5t^2\) \(5t^2\ -\ 30\sqrt{2}t\ +\ 50\ =\ 0\) \(D\ =\ (30\sqrt{2})^2\ -\ 4\cdot5\cdot50\ =\ 1800\ -\ 1000\ =\ 800\) \(t_1\ =\ \frac{30\sqrt{2}\ +\ \sqrt{800}}{2\cdot5}\ \approx\ 1.4\ с\) \(t_2\ =\ \frac{30\sqrt{2}\ -\ \sqrt{800}}{2\cdot5}\ \approx\ 7\ с\) Мы получили два ответа, так как уравнение является квадратным. Тело действительно проходит эту высоту два раза, до подъема и во время падения. Нам нужно ближайшее значение, поэтому рассматриваем время равное \(1.4\ с\). Движение по оси \(Ох\) равномерное с постоянной скоростью. Уравнение перемещения будет $$s\ =\ v_xt\ =\ v_0\cos\alpha\cdot t\ =\ 60\cdot\frac{\sqrt{2}}{2}\cdot 1.4\ с\ =\ 59.39\ м\ \approx\ 60\ м$$ \(Ответ: s = 60\ м\)

4.C вышки бросили камень в горизонтальном направлении. Через (2\ с) тело упало на расстоянии (30\ м) от вышки. С какой скоростью он упал?

\(Дано:\) \(t = 2\ с\) \(g = 10\ м/с^2\) \(l =\ 30\ м\) \(Найти: v = ?\)

\(Решение:\) Тело было подброшено горизонтально. Движение по оси \(Ох\) будет равномерным и за счет расстояния и времени полета тела можно найти скорость тела по этой оси. $$l=v_xt \quad \quad \Rightarrow \quad \quad v_x\ =\ \frac{l}{t}\ =\ 15\ м/с$$ Она будет постоянна и даже в момент падения равна \(15\ м/с.\) Чтобы найти значение скорости, нужно найти и скорость по оси \(Оу.\) Начальной скорости по этой оси не будет, так как начальная скорость не имеет проекции на ось \(Оу.\) Движение равноускоренное. Уравнение скорости будет: $$v_y\ =\ gt\ =\ 10*2\ =\ 20\ м/с$$ Зная значения проекция по формуле полученной благодаря теореме Пифагора найти модуль самой скорости. $$ v\ =\ \sqrt{v_x^2\ +\ v_y^2}\ =\ \sqrt{15^2\ +\ 20^2}\ =\ \sqrt{625}\ =\ 25\ м/с$$ \(Ответ: v = 25\ м/с\)

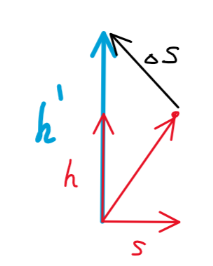
5.Два тела брошены одновременно из одной точки: одно вертикально вверх, другое под углом \(60°\) к горизонту. Начальная скорость каждого тела \(25\ м/с\). Найдите расстояние между телами спустя время \(1,7\ с.\)

\(Дано:\) \(v_0\ =\ 25\ м/с\) \(\alpha\ =\ 60°\) \(g = 10\ м/с^2\) \(t =\ 1.7\ с\) \(Найти: \Delta s = ?\)

\(Решение:\) Для нахождения расстояния тел через 1.7 с, найдем перемещение каждого тела с начальной точки и найдем векторную разницу между перемещениями. Первое тело брошено вверх. Тело будет перемещаться только по вертикали. Уравнение перемещения по вертикали у первого тела будет: $$h'\ =\ v_0t-\frac{gt^2}{2}\ =\ 25\cdot1.7 \ -\ \frac{10\cdot1.7^2}{2}\ =\ 28.05\ м$$ Второе тело подброшенное под углом к горизонту будет перемещаться как по оси \(Ох\) так и по оси \(Оу.\) Найдем перемещения по каждой оси: $$h\ =\ v_{0y}t\ -\ \frac{gt^2}{2}\ =\ v_{0}\sin\alpha\cdot t\ -\ \frac{gt^2}{2}\ =\ 25\cdot\frac{1}{2}\cdot1.7\ -\ \frac{10\cdot1.7^2}{2}\ =\ 6.8\ м$$ $$s\ =\ v_xt\ =\ v_{0x}t\ =\ v_0\cos\alpha\cdot t\ =\ 25\cdot\frac{\sqrt{3}}{2}\cdot1.7 \approx 36.8\ м$$ $$\Delta s\ =\ \sqrt{(h\ -\ h')^2\ +\ (s\ -\ s')^2}\ =\ \sqrt{(6.8\ -\ 28.05)^2\ +\ (36.8\ -\ 0')^2}\ \approx\ 36.8\ м$$ \(Ответ: \Delta s = 36.8\ м\)