Законы отражения и преломления света

Геометрическая оптика — раздел физики, изучающий распространение света в виде лучей. В ней рассматриваются такие явления, как отражение, преломление, образование изображения.

Световой луч — воображаемая прямая, вдоль которой распространяется свет.
Точечный источник света — объект, размеры которого малы по сравнению с расстоянием до препятствий.
Закон прямолинейного распространения света — в однородной среде свет распространяется по прямой.
Тень — область, в которую не попадает свет из-за преграды.

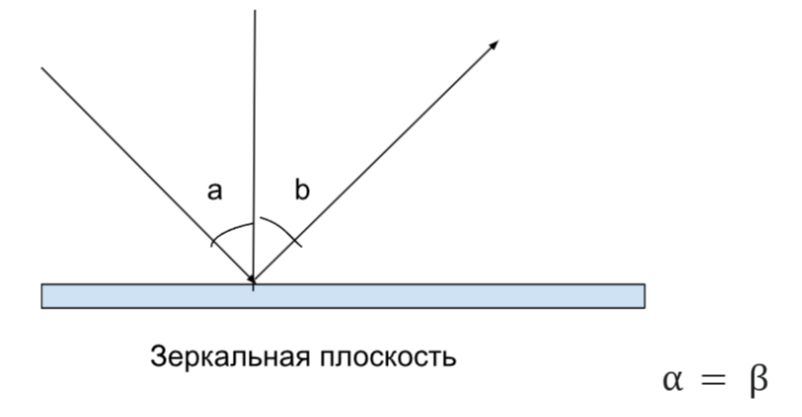
Закон отражения света:

Угол падения равен углу отражения: $$ \angle \alpha = \angle \beta $$
Падающий луч, отражённый луч и перпендикуляр к поверхности лежат в одной плоскости.

Отражение в плоском зеркале:

Изображение — мнимое, симметрично расположено за зеркалом.
Расстояние до изображения от зеркала равно расстоянию до предмета.

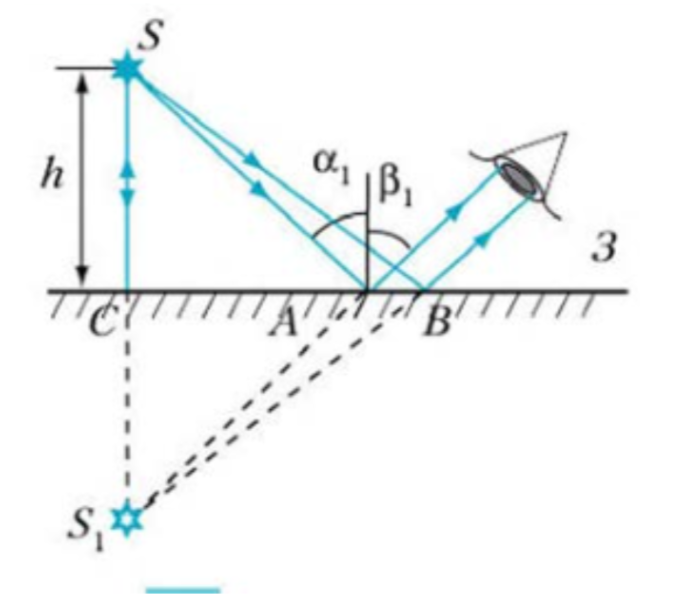
Построение изображения в плоском зеркале

Построить отражённые лучи от крайних точек предмета.
Провести продолжения отражённых лучей за зеркало.
Точка пересечения — мнимое изображение.

Закон преломления света- когда свет переходит из одной среды в другую, он изменяет направление:

$$ n_1 \sin \theta_1 = n_2 \sin \theta_2 $$

где:

$ n_1,\ n_2 $ — показатели преломления,
$ \theta_1,\ \theta_2 $ — углы падения и преломления.

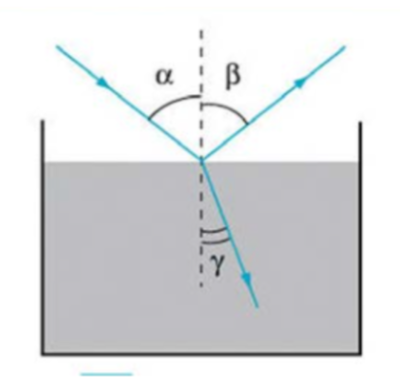
Полное внутреннее отражение-если $ n_1 > n_2 $, то существует предельный угол $\theta_{\text{кр}} $, при котором свет полностью отражается внутрь среды:

$$ \sin \theta_{\text{кр}} = \frac{n_2}{n_1} $$

Сферические зеркала

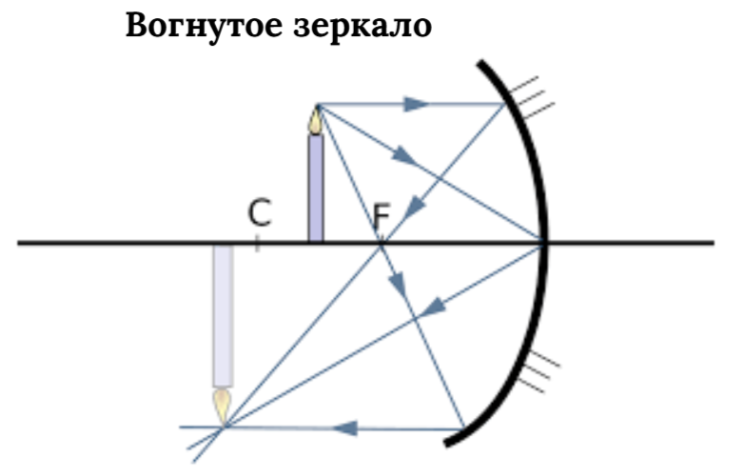
Вогнутое зеркало:

Фокус $ F = \frac{R}{2} $,
Изображение может быть действительным или мнимым,
Лучи: параллельный → через фокус, через фокус → параллельно, через центр → обратно.

Формула зеркала:

$$ \frac{1}{f} + \frac{1}{d} = \frac{1}{F} $$

где:

$ f $ — расстояние до изображения,
$ d $ — расстояние до предмета,
$ F $ — фокусное расстояние.

Выпуклое зеркало:

Фокус мнимый,
Изображения — всегда мнимые, уменьшенные,
Все лучи отражаются так, как если бы они исходили из фокуса.

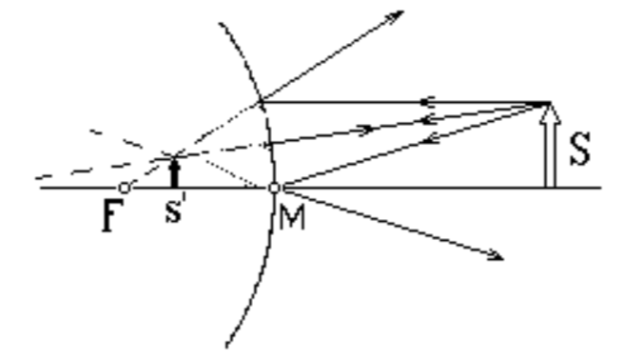
Формула для выпуклого зеркала:

$$ \frac{1}{f} + \frac{1}{d} = -\frac{1}{F} $$

Оптическая сила — характеристика зеркала, обратно пропорциональна фокусному расстоянию:

$$ D = \frac{1}{F} $$

Примеры решения задач

1.Найдите угол, под которым луч будет распространяться, выйдя из воды в воздух, если на границу раздела он упал под углом $ \frac{1}{6} \pi $ радиан. Показатель преломления воды $n_2 = 1.33$, воздуха $n_1 = 1.0$.

$ Дано:$
$ \theta_2 = \frac{1}{6}\pi = 30^\circ $
$ n_2 = 1.33 $
$ n_1 = 1.0 $
$ Найти:\ \theta_1 = ? $

$ Решение:$ Закон преломления: $$ n_2 \sin \theta_2 = n_1 \sin \theta_1 $$ Подставим: $$ 1.33 \cdot \sin(30^\circ) = 1.0 \cdot \sin \theta_1 $$ $$ 1.33 \cdot 0.5 = \sin \theta_1 $$ $$ \sin \theta_1 = 0.665 $$ Тогда: $$ \theta_1 = \arcsin(0.665) \approx 41.8^\circ $$
$ Ответ:\ \theta_1 \approx 41.8^\circ $

2.Радиус кривизны вогнутого сферического зеркала равен $2\ \text{м}$. Предмет находится на расстоянии $1.1\ \text{м}$ от зеркала.Найдите расстояние между предметом и его изображением.

$ Дано:$
$ R = 2\ \text{м} $
$ d = 1.1\ \text{м} $
$ Найти:\ \Delta = |f - d| $

$ Решение:$ Найдём фокусное расстояние: $$ F = \frac{R}{2} = 1\ \text{м} $$ Формула зеркала: $$ \frac{1}{f} + \frac{1}{d} = \frac{1}{F} $$ $$ \frac{1}{f} = \frac{1}{1} - \frac{1}{1.1} = \frac{1.1 - 1}{1.1} = \frac{0.1}{1.1} \approx 0.0909 $$ $$ f \approx 11\ \text{м} $$ Расстояние между предметом и изображением: $$ \Delta = |f - d| = |11 - 1.1| = 9.9\ \text{м} $$
$ Ответ: \ \Delta = 9.9\ м $

3.Радиус сферического вогнутого зеркала равен $1\ \text{м}$. Свеча высотой $10\ \text{см}$ расположена на расстоянии $0.75\ \text{м}$ от зеркала.Найдите высоту изображения этой свечи.

$ Дано:$
$ R = 1\ \text{м} $
$ d = 0.75\ \text{м} $
$ h = 0.1\ \text{м} $
$ Найти:\ h' = ? $

$ Решение:$ Найдём фокус: $$ F = \frac{R}{2} = 0.5\ \text{м} $$ Формула зеркала: $$ \frac{1}{f} + \frac{1}{d} = \frac{1}{F} $$ $$ \frac{1}{f} = \frac{1}{0.5} - \frac{1}{0.75} = 2 - \frac{4}{3} = \frac{2}{3} $$ $$ f = \frac{3}{2} = 1.5\ \text{м} $$ Увеличение (коэффициент масштаба): $$ k = \frac{f}{d} = \frac{1.5}{0.75} = 2 $$ Размер изображения: $$ h' = k \cdot h = 2 \cdot 0.1 = 0.2\ \text{м} $$
$ Ответ:\ h' = 0.2\ \text{м},\ \text{изображение увеличено в 2 раза} $
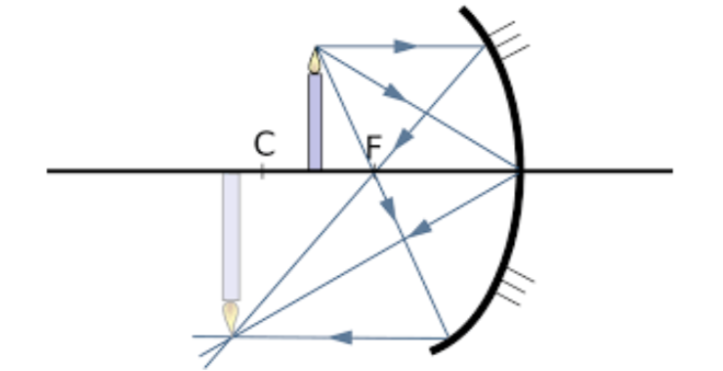