Оптические свойства линз: законы и формулы

Лучи света — линии, вдоль которых распространяется энергия света.
Линзы — прозрачные тела, у которых хотя бы одна из поверхностей не является плоской.

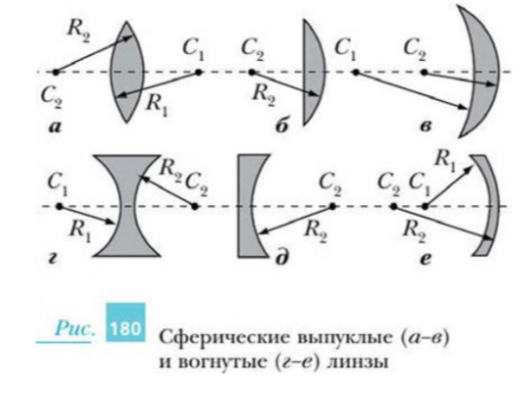
Виды линз

Выпуклая линза — середина толще краёв. Является собирающей линзой (если $ n_{отн} > 1 $).
Вогнутая линза — края толще середины. Является рассеивающей линзой (если $ n_{отн} > 1 $).

Если $ n_{отн} < 1 $, то свойства линз меняются на противоположные.

Оптическая сила линзы $ D $ — величина, обратная фокусному расстоянию:

$$ D = \frac{1}{F} $$

Из формулы тонкой линзы:

$$ D = (n_{отн} - 1)\left(\frac{1}{R_1} + \frac{1}{R_2}\right) $$

где:

$ R_1, R_2 $ — радиусы кривизны поверхностей линзы,
$ n_{отн} = \frac{n_2}{n_1} $ — относительный показатель преломления.

Единица измерения: диоптрия (дптр).

У собирающей линзы $ D > 0 $, у рассеивающей $ D < 0 $.

Фокус и оптические оси

Главная оптическая ось — прямая, проходящая через центр линзы и её поверхности.
Фокус линзы $ F $ — точка, в которой собираются (или из которой расходятся) лучи после прохождения через линзу.

Построение изображения линзой

Для построения изображения достаточно двух из трёх основных лучей:

Луч, идущий параллельно главной оси — после линзы пройдёт через фокус (для собирающей) или выйдет так, будто вышел из фокуса (для рассеивающей).
Луч, проходящий через фокус — после линзы выйдет параллельно главной оси.
Луч, проходящий через оптический центр — не меняет направления.

Изображение находится в точке пересечения двух построенных лучей (или их продолжений).

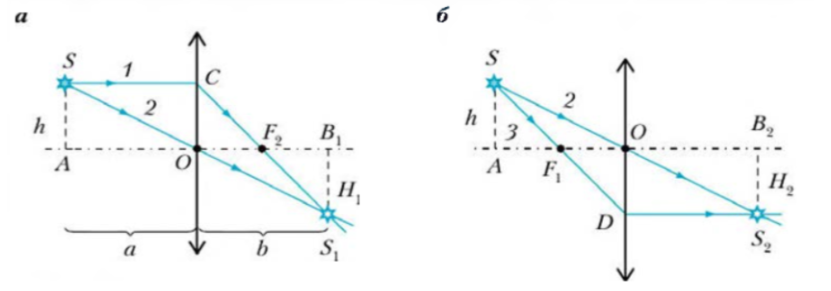
Формула тонкой линзы

$$ \frac{1}{F} = \frac{1}{d} + \frac{1}{f} $$

где:

$ d $ — расстояние от предмета до линзы,
$ f $ — расстояние от линзы до изображения,
$ F $ — фокусное расстояние.

Важно: учитывать знаки величин:

$ F < 0 $ — для рассеивающей линзы,
$ f < 0 $ — для мнимого изображения,
$ d > 0 $ — всегда.

Увеличение линзы

Отношение высоты изображения $ H_1 $ к высоте предмета $ h $:

$$ \gamma = \frac{H_1}{h} = \frac{f}{d} $$

Глаз как оптическая система

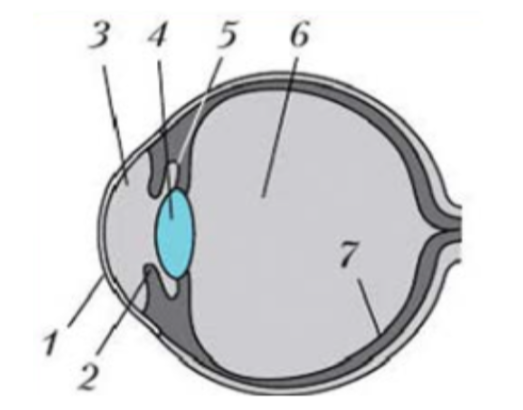
Роговица
Радужная оболочка
Прозрачная водянистая масса
Хрусталик
Мышцы, меняющие форму хрусталика
Стекловидное тело
Сетчатка глаз

Нарушение аккомодации приводит к близорукости или дальнозоркости. Исправляется линзами.

Примеры решения задач

1. Известно, что расстояние от источника света до линзы равно 0.05 м, при этом четкое изображение получается на экране на расстоянии 5 м от линзы. Найдите фокусное расстояние и оптическую силу линзы.

Дано:
$ d = 0.05\ м $
$ f = 5\ м $
Найти: $ F = ?,\ D = ? $

Решение:
Используем формулу тонкой линзы: $$ \frac{1}{F} = \frac{1}{d} + \frac{1}{f} $$ $$ \frac{1}{F} = \frac{1}{0.05} + \frac{1}{5} = 20 + 0.2 = 20.2 $$ $$ F = \frac{1}{20.2} \approx 0.0495\ м $$ Оптическая сила: $$ D = \frac{1}{F} = \frac{1}{0.0495} \approx 20.2\ дптр $$ Ответ: $ F \approx 0.0495\ м,\ D \approx 20.2\ дптр $

2. Человек носит очки с оптической силой -2,25 дптр. Каково для него расстояние наилучшего зрения без очков? Известно, что расстояние наилучшего зрения при нормальном зрении $ d_0 = 0.25\ м $.

$ Дано:$
$ D_{\text{очков}} = -2.25 \, \text{дптр} $
$ d_0 = 0.25 \, \text{м} $
$ Найти: d_z = ? $

$ Решение:$
Используем формулу для определения расстояния наилучшего зрения без очков: $$ \frac{1}{d_z} = \frac{1}{d_0} - D_{\text{очков}} $$ Подставим значения: $$ \frac{1}{d_z} = \frac{1}{0.25} - (-2.25) = 4 + 2.25 = 6.25 $$ Найдём расстояние: $$ d_z = \frac{1}{6.25} = 0.16 \, \text{м} $$ $ Ответ: \ d_z = 0.16 \, \text{м} $

3. Пучок параллельных лучей, распространяющихся в стекле, попадает на дефект. (Пузырек с воздухом, попавший в стекло при изготовлении) Радиус пузырька 1 см. Найдите на каком расстоянии после дефекта лучи (или их продолжения) сойдутся в одной точке.
$n_1=1.5$ (для стекла), $n_2=1$ (для воздуха)

Дано:
$ n_1 = 1.5 $
$ n_2 = 1 $
$ R = 1\,\text{см} = 0.01\,\text{м} $
Найти: $ F = ? $

Решение:
Внутри стекла находится пузырек воздуха — это сферическая выпуклая линза (тело с меньшим показателем преломления внутри среды с большим).
Формула фокусного расстояния для сферического дефекта (выпуклая сферическая поверхность): $$ \frac{1}{F} = \left( \frac{n_2}{n_1} - 1 \right) \cdot \frac{2}{R} $$ Подставим значения: $$ \frac{n_2}{n_1} = \frac{1}{1.5} = 0.\overline{6},\quad 0.\overline{6} - 1 = -0.333 $$ $$ \frac{1}{F} = -0.333 \cdot \frac{2}{0.01} = -0.333 \cdot 200 = -66.6 $$ $$ F = -\frac{1}{66.6} \approx -0.015\, \text{м} = -1.5\, \text{см} $$ Минус говорит о том, что лучи сходятся по ту сторону пузырька — в сторону падения лучей.
Ответ: $ F \approx -1.5\, \text{см} $