Работа электрического поля по перемещению заряда. Потенциал, разность потенциалов электрического поля.

Основные термины:

• Электрический потенциал
• Разность потенциалов (напряжение)
• Pабота электрического поля
• Эквипотенциальная поверхность
• Электрическое напряжение
• Потенциальная энергия заряда

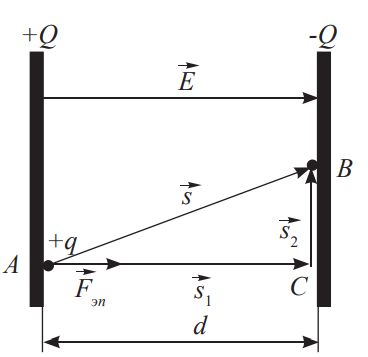
Пусть положительный заряд \(q\) под действием силы электрического поля заряженных пластин переместился из точки \(А\) одной пластины в точку \(B\) другой пластины, расстояние между пластинами \(d\). Работа, совершенная полем по перемещению заряда, будет равна $$A = FS cos \alpha$$ Сила действующая на заряд со стороны электрического поля будет \(F = qE\) И из графика будет \(cos \alpha = \frac{d}{S}\). Поэтому получаем: $$A = qEd$$ Работа однородного поля по перемещению заряда в нем из одной точки в другую не зависит от траектории движения. Она зависит только от положения этих точек в поле.

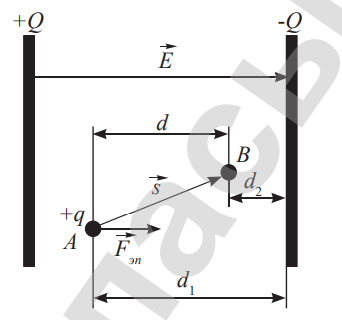
Поля, работа которых по перемещению тела по замкнутому контуру равна нулю, называют потенциальными. Такими полями являются гравитационное поле и электрическое поле, созданное неподвижным зарядом. Работу потенциального поля можно определить по изменению потенциальной энергии тела: $$A = - (\ W_{p2}\ -\ W_{p1} )$$ Пусть точки А и B − это произвольные точки поля, которые находятся на расстоянии \(d_1\) и \(d_2\) от пластины. Выразим отрезок \(d\) через эти расстояния: $$d\ =\ d_1\ –\ d_2$$ тогда $$A = – ( qEd_2 – qEd_1) $$. Из формул следует, что потенциальная энергия заряженного тела в однородном поле равна: $$ W_p = qEd$$ Потенциальная энергия заряженного тела в некоторой точке равна работе поля по перемещению заряда из этой точки поля в бесконечность.

Потенциальная энергия взаимодействия двух зарядов на расстоянии \(r\) в среде будет найдена по формуле: $$W_p = \frac{k q_1 q_2}{\varepsilon r}$$ Знак будет зависеть от знаков зарядов. Потенциал электрического поля - скалярная величина, равная отношению потенциальной энергии заряда в заданной точке поля к величине этого заряда: $$\varphi = \frac{W_p}{q} \quad \quad \quad \quad [В]$$ Он может принимать положительные или отрицательные значения. Физический смысл имеет разность потенциалов поля, так как через нее выражается работа сил поля по перемещению заряда.
Для однородного электрического поля потенциал точки поля равен: $$\varphi = \frac{q E d}{q} = Ed \quad \quad \quad \quad \varphi = \frac{kQ}{\varepsilon r}$$ \(Q\ -\ точечный\ заряд\ создавший\ это\ поле\)
\(r\ -\ расстояние\ от\ заряда\ Q\ до\ точки \)

Разность потенциалов (напряжение) - физическая величина, равная отношению работы электрического поля по перемещению положительного заряда из одной точки поля в другую к величине этого заряда, называется разностью потенциалов или напряжением. $$A = qEd_1 - qEd_2 = q \varphi_1 \ -\ q \varphi_2 = q (\varphi_1 \ - \ \varphi_2)$$

Эквипотенциальная поверхность - поверхность, в каждой точке которой потенциал электрического поля имеет одно и то же значение. Перемещение заряда вдоль этой поверхности не требует работы. Электрическое напряжение-физическая величина, равная работе электрического поля по перемещению единичного заряда между двумя точками. Обычно измеряется в вольтах.

Потенциал поля, созданного несколькими зарядами, равен алгебраической сумме потенциалов полей каждого из них. $$\varphi\ =\ \varphi_1\ +\ \varphi_2\ +\ \dots \ + \varphi_n$$ Это выражение принципа суперпозиции полей для энергетической характеристики. Потенциал поля положительного заряда – положительный, отрицательного заряда − отрицательный.

Примеры решения задач:

1.Металлический шар радиусом \(18\ см\) заряжен до \(0,8\ нКл\). Чему равен потенциал поверхности шара.

2. Два точечных заряда \(q_1 = 6,6 \cdot 10^{–9}\ Кл\) и \(q_2 = 1,32 \cdot 10^{–8}\ Кл\) находятся на расстоянии \(r_1 = 40\ см\). Какую работу необходимо совершить, чтобы сблизить их до расстояния \(r_2 = 25\ см\)?

3.Электростатическое поле создано неподвижным точечным зарядом \(Q\). В точке, находящейся на расстоянии \(r = 80\ см\) от заряда, потенциал поля \(\varphi = 0,42\ кВ\). Определите модуль силы, действующей со стороны поля на точечный заряд \(q = 1,5\ нКл\), помещенный в эту точку.