• +7 777 150 51 51

Конденсаторы. Энергия заряженного конденсатора. Соединение конденсаторов.

Основные термины:

Электроемкость уединенного проводника \(C\) – это физическая величина, равная отношению заряда проводника к его потенциалу. $$C = \frac{q}{\varphi} \quad \quad [Ф]$$ Подставим в эту формулу расчета потенциала проводящей сферы \(\varphi = \frac{kq}{\varepsilon r}\), получим: $$C = \frac{\varepsilon r}{K} \quad \quad \quad \quad \quad или \quad \quad \quad \quad \quad C = 4 \pi \varepsilon_0 \varepsilon r$$ Чем больше радиус уединенной сферы, тем больше ее электроемкость. Полученные выводы верны и для шара, так как внутри проводников нет свободных зарядов и электрическое поле отсутствует.

Конденсатор – устройство для накопления заряда и энергии электрического поля. Состоит из двух пластин, разделенных диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Широкое применение получил плоский конденсатор, состоящий из двух плоских параллельных пластин, разделенных диэлектриком. Пластины конденсатора называют обкладками. Пластины представляют собой металлическую фольгу, диэлектриком могут служить бумага, слюда, лак. В зависимости от использованного материала различают бумажные, слюдяные, электролитические конденсаторы
Электроемкость конденсаторов будет найдена по формуле: $$C = \frac{\varepsilon \varepsilon_0 S}{d}$$ \(\varepsilon_0 = 8.85 \cdot 10^{-12} \ Ф/м - постоянная\ величина\)
\(S - площадь\ обкладки\)
\(d - расстояние\ между\ обкладками\)
Диэлектрик - материал, помещаемый между пластинами конденсатора для увеличения его емкости и предотвращения пробоя.

На обкладках конденсатора накапливаются противоположные по знаку электрические заряды, модули которых равны. Процесс накапливания зарядов на обкладках называют зарядкой конденсатора, а процесс нейтрализации зарядов при соединении обкладок конденсатора проводником — разрядкой конденсатора. Модуль заряда, находящегося на одной из обкладок конденсатора, называют зарядом конденсатора. $$q = C U$$

Напряжение \(U\) - разность электрических потенциалов между пластинами конденсатора, измеряется в вольтах \(В\).
Энергия заряженного конденсатора - количество энергии, хранящееся в конденсаторе, когда он заряжен, измеряется в джоулях \(Дж\). $$W = \frac{q^2}{2C} = \frac{CU^2}{2} = \frac{qU}{2}$$

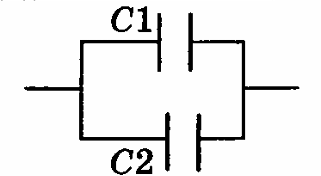
Последовательное соединение конденсаторов - способ соединения, при котором конденсаторы соединяются цепочкой, один за другим, приводя к уменьшению общей емкости. Параллельное соединение конденсаторов - способ соединения, при котором все конденсаторы подключаются к одной и той же паре точек, приводя к увеличению общей емкости.
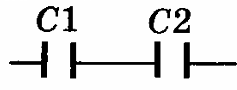
график график
$$U = U_1 + U_2 $$ $$U = U_1 = U_2$$
$$q = q_1 = q_2$$ $$q = q_1 + q_2$$
$$C = C_1 + C_2$$ $$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2}$$

Примеры решения задач:

1.Плоскому конденсатору электроемкостью \(C = 0,4\ мкФ\) сообщен электрический заряд \(q = 2\ нКл\). Определите модуль напряженности электростатического поля между обкладками конденсатора, если расстояние между ними \(d = 5\ мм.\)

\(Дано:\)
\( C = 0.4\ мкФ\ =\ 4 \cdot 10^{-7}\ Ф \)
\( q = 2\ нКл = 2 \cdot 10^{-9}\ Кл \)
\( d = 5\ мм = 5 \cdot 10^{-3}\ м\)

\( Найти:\ E = ? \) 		\(Решение:\)
По основной формуле электроемкости найдем значение напряжения: $$C = \frac{q}{U} \quad \quad \quad \Rightarrow \quad \quad \quad U = \frac{q}{C}$$ Для нахождения напряженности используем формулу связи между силовой и энергетической характеристики поля: $$E = \frac{U}{d} = \frac{q}{Cd} = \frac{2 \cdot 10^{-9}}{4 \cdot 10^{-7} \cdot 5 \cdot 10^{-3}} = 0,1 \cdot 10^{1} = 1\ \frac{В}{м}$$

\(Ответ:\ 1\ \frac{В}{м}\)

2. Какой заряд имеют обкладки воздушного конденсатора площадью \(200\ см^2\) каждая, если расстояние между обкладками \(0,1\ см\), а разность потенциалов \(600\ В\)?

\(Дано:\)
\( U = 600\ В\)
\( S = 200\ см^2 = 200 \cdot 10^{-4}\ м^2\)
\( d = 0.1\ см = 1 \cdot 10^{-3}\ м\)

\( Найти:\ q = ? \) 		\(Решение:\)
Преобразуем основную формулу электроемкости для нахождения заряда: $$C = \frac{q}{U} \quad \quad \quad \Rightarrow \quad \quad \quad q = CU$$ Подставим вместо электроемкости \(C\) формулу плоского конденсатора в котором \(\varepsilon = 1\) так как это воздушный конденсатор: $$C = \frac{\varepsilon_0 S}{d}$$ $$q = C U = \frac{\varepsilon_0 S \cdot U}{d} = \frac{8.85 \cdot 10^{-12} \cdot 200 \cdot 10^{-4} \cdot 600}{1 \cdot 10^{-3}} = 1062 \cdot 10^{-10}\ Кл = 106,2\ нКл$$

\(Ответ:\ 106,2\ нКл\)

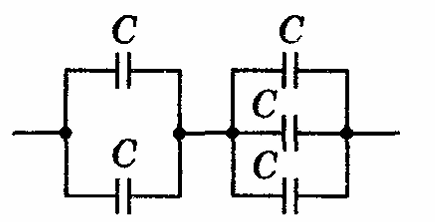
3. Найдите общую электроемкость схемы. Емкости всех конденсаторов равны \(1\ мкФ\)

\(Дано:\)
\( C = 1\ мкФ = 1 \cdot 10^{-6}\ Ф\)

\(Найти:\ C_{общ} = ?\) 		график \(Решение:\)
Первые два конденсатора слева соединены параллельным образом и их общая электроемкость будет найдена по обратной сумме: $$\frac{1}{C_{12}} = \frac{1}{C} + \frac{1}{C} = \frac{2}{C} \quad \quad \Rightarrow \quad \quad C_{12} = \frac{C}{2}$$ Три конденсатора справа также соединены параллельно, поэтому: $$\frac{1}{C_{345}} = \frac{1}{C} + \frac{1}{C} + \frac{1}{C} = \frac{3}{C} \quad \quad \Rightarrow \quad \quad C_{345} = \frac{C}{3}$$ Две группы между собой соединены последовательно, и их общая электроемкость будет найдена по сумме: $$C_{} = C_{12} + C_{345} = \frac{C}{2} + \frac{C}{3} = \frac{3C + 2C}{6} = \frac{5C}{6} = \frac{5 \cdot 1 \cdot 10^{-6}}{6} \approx 0.83 \cdot 10^{-6}\ Ф = 0,83\ мкФ$$

\(Ответ:\ 0,83\ мкФ\)