lessons.kz
Физика ЕНТ
Электростатика
Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрического поля.

Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрического поля.

Основные термины:

Электрическое поле
Напряженность электрического поля
Линии электрического поля
Точечный заряд
Принцип суперпозиции электрических полей
Электрический диполь

Электрическое поле - область вокруг электрического заряда, в которой другие заряды испытывают электрическую силу. Это поле представляет собой модель для объяснения взаимодействия между зарядами на расстоянии.
Свойства электрического поля:

материально, т. е. существует независимо от нашего сознания;
возникает вокруг зарядов и обнаруживается по действию на пробный заряд;
непрерывно распределено в пространстве;
ослабевает по мере удаления от заряда;
скорость распространения электрического поля в вакууме равна скорости света

Напряженность электрического поля $E$ - векторная величина, которая описывает электрическое поле в данной точке. Она определяется как сила, действующая на единичный положительный заряд(силовая характеристика эл. поля) помещенный в эту точку, и измеряется в вольтах на метр $ [В / м]$. $$E = \frac{F}{q} = k \frac{Q}{\varepsilon R^2}$$

$E - напряженность\ [B]$
$F -\ сила\ [Н]$
$q -\ заряд\ [Kл]$

Направление вектора напряженности совпадает с направлением силы Кулона, если пробный заряд положительный: $q > 0 \quad \vec{F} \uparrow \uparrow \vec{E}$

Силовые линии - линии, касательные к которым совпадают с вектором напряженности.

Направление силовой линии совпадает с направлением вектора напряженности.
Чем гуще силовые линии, тем сильнее электрическое поле.
Линии напряженности начинаются на положительных зарядах, а заканчиваются на отрицательных или на бесконечности.
Если силовые линии поля параллельны, то поле называют однородным.

Напряженность однородного электрического поля прямо пропорциональна напряжению между пластинами и обратно пропорциональна расстоянию между ними. (пригодится в задачах с электроемкостью и конденсаторами) $$ E = \frac{U}{d}$$
$где\ U\ -\ напряжение\ [В]$
$d\ -\ расстояние\ между\ пластинами\ [м]$

Точечный заряд - идеализированная модель заряда, который настолько мал, что его размер можно считать бесконечно малым по сравнению с расстоянием до точки наблюдения. Это упрощение позволяет анализировать электрическое поле без учета геометрических размеров заряда.

Принцип суперпозиции электрических полей - утверждение о том, что в случае присутствия нескольких зарядов, напряженность результирующего электрического поля в любой точке является векторной суммой напряженностей полей, создаваемых каждым зарядом в отдельности

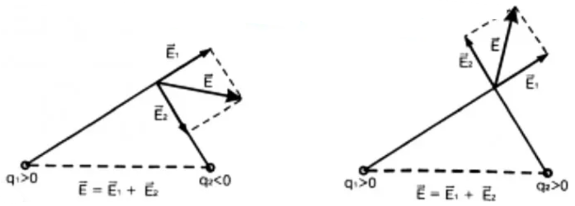
$$\vec{E} = \vec{E_1} + \vec{E_2} + \dots + \vec{E_n} \quad \quad \quad где\ E_i = \frac{kq_i}{R_i^2}$$

Электрический диполь - пара равных по модулю, но противоположных по знаку зарядов, находящихся на определенном расстоянии друг от друга. Электрическое поле диполя имеет особую конфигурацию. является векторной суммой напряженностей всех отдельных полей, создаваемых в этой точке каждым зарядом в отдельности.

Примеры решения задач:

1. Определите величину заряда, если известно, что в электрическом поле напряженностью $5\ кВ/м$ на заряд действует сила $30\ Н$.

$Дано :$
$ E = 5\ кВ/м = 5 \cdot 10^3 \ В/м $
$ F = 30\ Н $

$Найти:\ q = ? $

$Решение:$
Используем основную формулу напряженности. Преобразовываем его для нахождения заряда: $$E = \frac{F}{q} \quad \quad \quad \Rightarrow \quad \quad \quad q = \frac{F}{E} = \frac{30}{5 \cdot 10^3} = 6 \cdot 10^{-3}\ Кл = 6\ мКл$$

$Ответ:\ 6\ мКл$

2. Два заряда $10\ мкКл$ и $6\ мкКл$ находятся на расстоянии $2\ м$. Найдите модуль напряженности электрического поля в середине отрезка, соединяющего эти заряды.

$Дано :$
$ q_1 = 10\ мкКл = 10^{-5}\ Кл$
$ q_2 = 6\ мкКл = 6 \cdot 10^{-6}\ Кл$
$ r = 2\ м $

$Найти:\ E = ? $

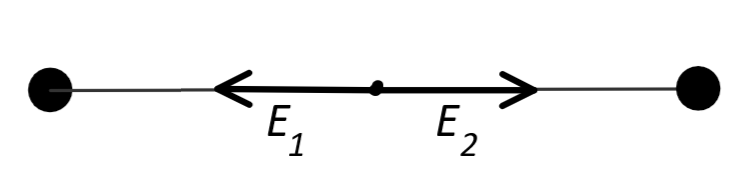
Численное значение будет найдено по формуле $E_1 = k \frac{q_1}{r_1^2} \quad \quad \quad E_2 = k \frac{q_2}{r_2^2}$
Значение первого заряда больше $q_1 > q_2 \quad \quad \Rightarrow\quad \quad E_1 > E_2$ Поэтому результирующий вектор будет направлен в ту же сторону и значение будет найдено как: $$\vec{E} = \vec{E_1} + \vec{E_2} \quad \quad \quad E = E_1 - E_2 $$ $$E = k \frac{q_1}{r_1^2} - k \frac{q_2}{r_2^2} = \frac{9 \cdot 10^9 \cdot 10^{-5}}{1^2} - \frac{9 \cdot 10^9 \cdot 6 \cdot 10^{-6}}{1^2} = 9 \cdot 10^4 - 5.4 \cdot 10^4 = 3.6 \cdot 10^4\ Н/Кл$$

$Ответ:\ 3.6 \cdot 10^4\ Н/Кл$

3. Два точечных заряда $+5q$ и $-2q$ находятся на расстоянии $10\ см$ друг от друга. В какой точке прямой, проходящей эти заряды, напряженность электрического поля будет равно нулю.

$Дано :$
$q_1 = +5q$
$q_2 = -2q$
$r = 10\ см = 0,1\ м$
$E = 0$

$Найти:\ r = ? $

$Решение:$
По принципу суперпозиции полей строим векторы напряженности $E_1$ и $E_2$ в каждом поле созданном отдельно зарядами $q_1$ и $q_2$ и суммируем векторно. Для того чтобы сумма векторов была равна нулю необходимо чтобы они были противоположны друг другу и численно равны. Относительно зарядов мы можем получить три разных местоположения точек.
график

Так как значение $ |q_1| > |q_2| $ то численное значение напряжение будет зависеть от заряда и численно они могут быть равными только если $r_1 > r_2$ поэтому нам нужно рассматривать третий случай.
Возьмем расстояние от точки к второму заряду как $x$. Тогда $r_1 = r + x \quad r_2 = x$ $$\vec{E} = \vec{E_1} + \vec{E_2} \quad \quad \quad E = E_1 - E_2 \quad \quad \Rightarrow\quad \quad 0 = E_1 - E_2 \quad \quad \Rightarrow\quad \quad E_1 = E_2 $$ $$ k \frac{q_1}{r_1^2} = k \frac{q_2}{r_2^2} $$ $$\frac{5q}{( 0.1 + x)^2} = \frac{2q}{x^2}$$ $$\frac{5}{( 0.1 + x)^2} = \frac{2}{x^2}$$ $$5x^2 = 2(0.1 + x)^2$$ $$5x^2 = 0.02 + 0.4x + 2x^2$$ $$3x^2 - 0.4x - 0.02 = 0$$ Квадратное уравнение решаем дискриминантом и получаем ответ $x = 0.17\ м $.

$Ответ:\ 0,17\ м\ от\ отрицательного\ заряда$