Переменный ток. Закон Ома. Мощность. Трансформаторы

Колебательный контур содержит катушку индуктивности (L) и конденсатор ёмкости (C). При замыкании ключа энергия переходит из электрической в магнитную и обратно.

$$ W_0 = \frac{L I_{\max}^2}{2} = \frac{C U_{\max}^2}{2}, \qquad \omega_0 = \frac{1}{\sqrt{LC}}, ; T = 2\pi\sqrt{LC}. $$

Зависимость тока и заряда во времени:

$$Q(t) = Q_{\max}\cos(\omega_0 t), \qquad I(t) = -I_{\max}\sin(\omega_0 t).$$

Конденсатор в AC–цепи

Напряжение источника:
$$U(t) = U_{\max}\cos(\omega t).$$ Напряжение на конденсаторе совпадает с напряжением источника:
$$U_C = U(t).$$ Заряд:
$$q = C U_C = C U_{\max}\cos(\omega t).$$ Сила тока:
$$I = \frac{dq}{dt} = -\omega C U_{\max}\sin(\omega t) = I_{\max}\cos\left(\omega t - \frac{\pi}{2}\right).$$ Амплитуда тока:
$$I_{\max} = \omega C U_{\max}.$$
Реактивное сопротивление конденсатора:
$$X_C = \frac{1}{\omega C}.$$
Фаза напряжения опережает фазу тока на \(\frac{\pi}{2}\).

Индуктивность в AC–цепи

Напряжение источника:
$$U(t) = U_{\max}\cos(\omega t).$$ Ток в катушке:
$$I = I_{\max}\cos\left(\omega t - \frac{\pi}{2}\right).$$ Индуктивное напряжение:
$$U_L = L\frac{dI}{dt} = \omega L I_{\max}\sin(\omega t - \frac{\pi}{2}) = U_{\max}\cos(\omega t).$$ Амплитуда:
$$U_{\max} = \omega L I_{\max}.$$
Реактивное сопротивление катушки:
$$X_L = \omega L.$$
Фаза напряжения отстаёт от фазы тока на \(\frac{\pi}{2}\).

Закон Ома для полной RLC‑цепи

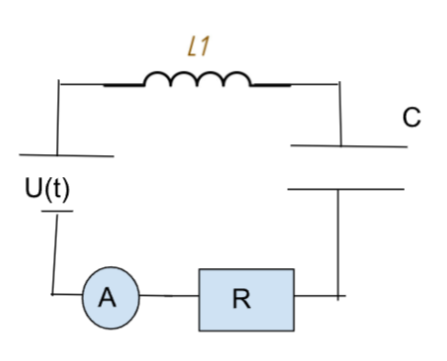
Последовательная цепь: резистор \(R\), индуктивность \(L\) и конденсатор \(C\). Полное сопротивление цепи: $$Z = \sqrt{R^2 + \left(X_L - X_C\right)^2} = \sqrt{R^2 + \left(\omega L - \frac{1}{\omega C}\right)^2}.$$ Амплитуда тока: $$I_{\max} = \frac{U_{\max}}{Z}.$$

Мощность переменного тока $$ I(t)=I_{\max}\cos(\omega t), \qquad U(t)=U_{\max}\cos(\omega t+\varphi). $$ Мгновенная мощность:
$$P(t) = I(t)U(t).$$ Средняя мощность за период:
$$P_{\text{ср}} = \frac{I_{\max}U_{\max}}{2}\cos\varphi = I_{\text{действ}}U_{\text{действ}}\cos\varphi.$$ \(\cos\varphi\) — коэффициент мощности.

Индукционный генератор

Ротор с постоянным магнитом создаёт переменное магнитное поле. Статор — катушки, в которых индуцируется ЭДС: $$E = -N\frac{d\Phi}{dt}$$

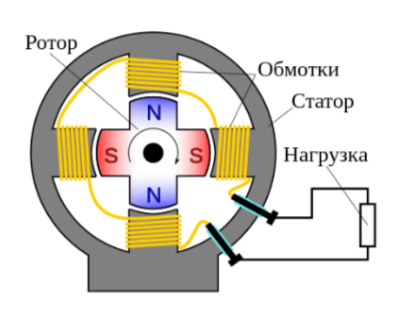
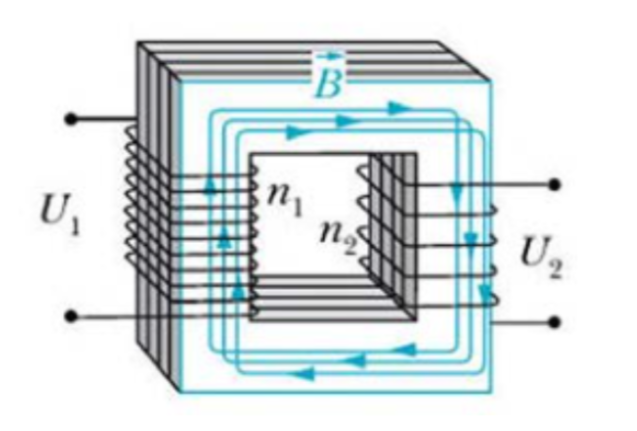
Трансформатор

Две катушки \(N_1, N_2\) на общем магнитопроводе: $$\frac{E_1}{E_2} = \frac{N_1}{N_2}.$$ Используется для повышения (передача по ЛЭП) или понижения (перед потребителем) напряжения.

Примеры решение задач:

1.Цепь состоит из источника и конденсатора. Источник тока работает по закону \(U=U_{max}\) \(cos(\omega t)\) где \(U_{max}\)=10 В, \(\omega\) =\(\frac {1}{3} \frac{1}{с}\). Емкость конденсатора С = 0.1 Фр. Найдите максимальное значение тока.

2.Для схемы, состоящей из катушки индуктивности и источника \(U=U_{max}\) \(cos(\omega t\)) где \(U_{max}=10\)В , \(\omega=\frac{1}{5} \frac{1}{с}\) найдите максимальное значение тока. L=10 Гн.

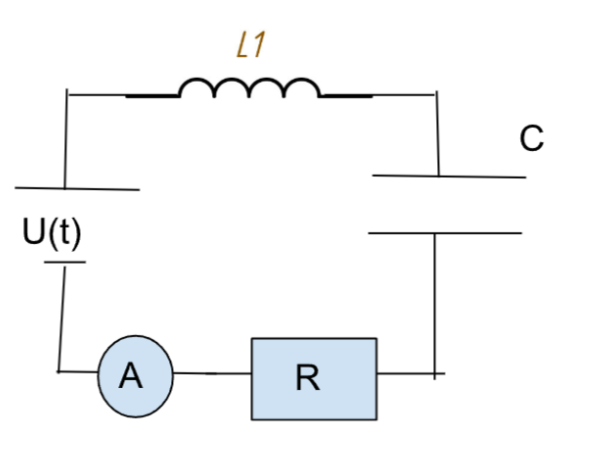
3.Найдите сопротивление цепи переменного тока и максимальное значение тока. R=10 Ом, L=10 Гн , С=10 Ф. Источник тока работает по закону \(U=U_{max} cos(\omega t)\) где \(U_{max}\)=15 В, \(\omega =\frac{1}{50} \frac {1}{с}\)

\( Дано:\) \(R = 10\,Ом\) \(L = 10\,Гн\) \(C = 10\,Ф\) \(U_{\max} = 15\,В\) \(\omega = \frac{1}{50}\,\text{с}^{-1}\) \( Найти: Z,\; I_{\max} = ? \)

\( Решение:\) Найдём реактивные сопротивления: \(X_L = \omega L = \frac{1}{50} \cdot 10 = 0.2\,Ом\) \(X_C = \frac{1}{\omega C} = \frac{1}{\frac{1}{50} \cdot 10} = 5\,Ом\) Полное сопротивление цепи: $$Z = \sqrt{R^2 + (X_L - X_C)^2} = \sqrt{10^2 + (0.2 - 5)^2} = \sqrt{100 + 23.04} \approx 11.09\,Ом.$$ Максимальный ток: $$I_{\max} = \frac{U_{\max}}{Z} = \frac{15}{11.09} \approx 1.35\,\text{А}.$$ \( Ответ: Z \approx 11.09\,Ом,\; I_{\max} \approx 1.35\,А \)