- +7 701 537 76 67
Основы переменного тока и электромагнитных колебаний
Колебательный контур включает катушку индуктивности \( L \) и конденсатор ёмкостью \( C \). После замыкания ключа энергия периодически переходит из электрической формы (конденсатор) в магнитную (катушка):
$$
W_0 = \frac{L I_{\max}^2}{2} = \frac{C U_{\max}^2}{2}.
$$
Циклическая частота и период:
$$
\omega_0 = \frac{1}{\sqrt{LC}}, \qquad T = 2\pi\sqrt{LC}.
$$
Зависимость заряда и тока от времени:
$$
Q(t)=Q_{\max}\cos(\omega_0 t), \qquad I(t)=-I_{\max}\sin(\omega_0 t).
$$
Энергия магнитного и электрического полей при свободных колебаниях
$$
W_0 = \frac{L I_{\max}^2}{2} = \frac{C U_{\max}^2}{2}.
$$
Для любого момента времени при незатухающих колебаниях:
$$
W_0 = \frac{L I^{2}(t)}{2} + \frac{C U^{2}(t)}{2}.
$$
Если контур подключён к источнику переменного напряжения
$$
U(t)=U_{\max}\cos(\omega_{\text{ист}} t),
$$
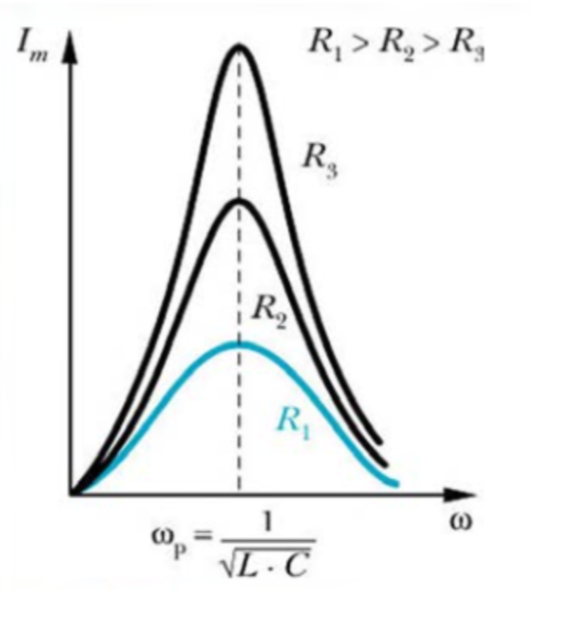
то колебания в контуре происходят с частотой \( \omega_{\text{ист}} \).
| Резонанс наступает, когда \( \omega_{\text{ист}} = \omega_0 = 1/\sqrt{LC} \); амплитуда тока и напряжения становится максимальной. |
|
|
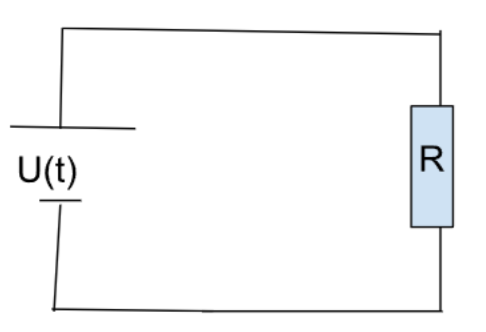
Активное сопротивление в цепи переменного тока Для цепи «источник + резистор» напряжение и ток совпадают по фазе: $$ U(t)=U_{\max}\cos(\omega t), \qquad I(t)=\frac{U_{\max}}{R}\cos(\omega t)=I_{\max}\cos(\omega t). $$ |
|
Мгновенная мощность на резисторе:
$$
P(t)=I^2(t) R = I_{\max}^2 R\cos^2(\omega t).
$$
Эффективные (действующие) значения-действующие значения определяют постоянные ток и напряжение, при которых за период выделяется та же энергия, что и при переменном токе:
$$
I_{\text{действ}} = \frac{I_{\max}}{\sqrt{2}}, \qquad U_{\text{действ}} = \frac{U_{\max}}{\sqrt{2}}.
$$
Средняя (активная) мощность:
$$
P_{\text{ср}} = I_{\text{действ}}^2 R = \frac{U_{\max}^2}{2R}.
$$
Примеры решения задач
1. Колебательный контур долго заряжают от источника с напряжением 5 \(В\). В момент времени \( t = 0 \) энергия в контуре 0.25 Дж, а максимальный ток в цепи \( I_{\max} = 0.2\pi , \text{А} \). Определить период и круговую частоту свободных колебаний.
|
\( Дано:\) \( U_{\max} = 5 \ \text{В} \) \( I_{\max} = 0.2\pi \ \text{А} \) \( W_0 = 0.25 \ \text{Дж} \) \( Найти: T,\; \omega_0 \) |
\( Решение: \) Энергия в момент заряда: $$ W_0 = \frac{C U_{\max}^2}{2} \Rightarrow C = \frac{2 W_0}{U_{\max}^2} = \frac{2 \cdot 0.25}{5^2} = 0.02 \ \text{Ф}. $$ Энергия через ток: $$ W_0 = \frac{L I_{\max}^2}{2} = \frac{L (0.2\pi)^2}{2} \Rightarrow L = \frac{2 W_0}{(0.2\pi)^2} = \frac{0.5}{0.04\pi^2} \approx 1.27 \ \text{Гн}. $$ Период собственных колебаний: $$ T = 2\pi\sqrt{LC} = 2\pi\sqrt{1.27 \cdot 0.02} \approx 2\pi \cdot 0.16 \approx 1.0 \ \text{с}. $$ Круговая частота: $$ \omega_0 = \frac{2\pi}{T} \approx 6.3 \ \text{рад/с}. $$ \( Ответ: T \approx 1.0 \ \text{с}, \; \omega_0 \approx 6.3 \ \text{рад/с}. \) |
2. Как изменится период тока в контуре, если к конденсатору подключить ещё три точно таких же конденсатора параллельно?
|
\( Дано:\) \( C \) — начальная ёмкость; \( 3C \) — добавляют параллельно. \( Найти: T_{\text{нов}} / T_1 \) |
\( Решение: \) При параллельном соединении: $$ C_{\text{общ}} = 4C. $$ Период: \( T = 2\pi\sqrt{LC}. \) $$ T_{\text{нов}} = 2\pi\sqrt{L C_{\text{общ}}} = 2\pi\sqrt{4LC} = 2\,T_1. $$ \( Ответ: \) период увеличится в 2 раза. |
3. Сколько тепла выделится на резисторе \( R\) = 20 Ом за 1 минуту, если амплитудное напряжение источника
\( U_{\max}\)=60 \(B\)?
|
\( Дано: \) \( R = 20 \,Ом \) \( U_{\max} = 60 \, \text{В} \) \( t = 60 \, \text{с} \) \( Найти: Q = ? \) |
\( Решение: \) Действующее напряжение: $$ U_{\text{дей}} = \frac{U_{\max}}{\sqrt{2}}. $$ Мощность на резисторе: $$ P = \frac{U_{\text{дей}}^2}{R} = \frac{U_{\max}^2}{2R}. $$ Работа (теплота) за время \( t \): $$ Q = P t = \frac{U_{\max}^2}{2R} t = \frac{60^2}{2 \cdot 20} \cdot 60 = 180 \cdot 60 = 10800 \ \text{Дж}. $$ \( Ответ: Q = 10.8 \ \text{кДж}. \) |