Индуктивность. Самоиндукция. Энергия магнитного поля. Правило Ленца. Принцип действия электромагнитных приборов (электромагнитное реле, генератор).

Основные термины и необходимые понятия:

• Электромагнитной индукция
• Магнитный поток

Правило Ленца. Правило определения индукционного тока.

Индукционный ток в цепи имеет такое направление, что создаваемое им магнитное поле стремиться компенсировать вызвавшее этот ток изменение числа магнитных линий, которые проходят через плоскость, ограниченную этой цепью.

Рассмотрим пример с магнитом и катушкой.

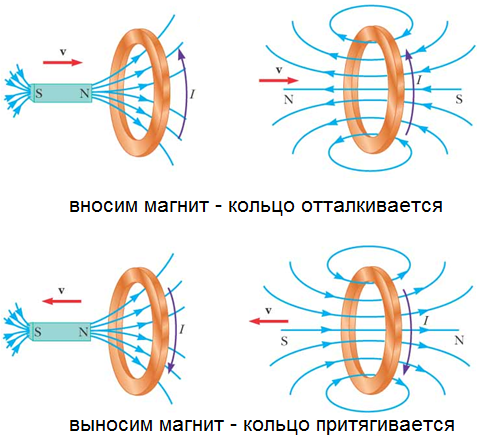
Катушку с (N) витками можно рассматривать как (N) рамок наложенных друг на друга. В каждой из рамок будет возникать ток из за изменения магнитного поля.

\(\Delta \Psi = \Delta (\vec{B} \cdot \vec{S}) = (\Delta \vec{B}) \cdot \vec{S}\) (так как площадь витка катушки не меняется)

\(E = -\frac{\Delta \Psi}{\Delta t} = -\frac{(\Delta \vec{B}) \cdot \vec{S}}{\Delta t}\) (ЭДС каждого витка)

\(\sum E = -\sum \left( \frac{\Delta \vec{B}}{\Delta t} \cdot \vec{S} \right) = -N \cdot \left( \frac{\Delta \vec{B}}{\Delta t} \cdot \vec{S} \right)\)

\(Где:\)

\(\sum E\ -\ Суммарный\ ЭДС\ возникающая\ в\ катушке,\)

\(N\ –\ количество\ витков,\)

\(\frac{\Delta \vec{B}}{\Delta t}\ -\ скорость\ изменения\ магнитной\ индукции.\)

Индуктивность.

Индуктивность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и полным магнитным потоком \(\Psi\), создаваемым этим током через поверхность, краем которой является данный контур.

$$\Psi = L \cdot I$$

\(Где:\ L\ –\ Индуктивность,\ I\ -\ ток\ в\ контуре.\)

\(Единицы\ измерения:\ Генри,\ Гн = \frac{В \cdot с}{А} = \frac{кг \cdot м^2}{с^2 \cdot А^2}.\)

Индуктивность – характеристика элемента цепи, или контура.

Связь индуктивности, скорости изменения тока и приложенного ЭДС.

Пусть к некоторой катушке, обладающую индуктивностью \(L\), подключили к ЭДС = \(U\). В катушку ток будет возрастать с некоторой скоростью \(\frac{\Delta I}{\Delta t}\), пока не достигнет некоторого максимального значения.

$$E_L = -L \cdot \frac{\Delta I}{\Delta t}$$

\(Где:\)

\(E_L\ –\ ЭДС,\ приложенная\ к\ катушке.\)

\(L\ –\ индуктивность\ катушки.\)

\(\frac{\Delta I}{\Delta t}\ –
скорость\ изменения\ тока.\)

Ток будет возрастать до значения \(I_{max}\). \(I_{max}\) зависит от значения сопротивления других элементов цепи.

$$ I_{max}\ = \frac{U}{R_{цепи}}$$

Расчет индуктивности катушки.

Рассмотрим цилиндрическую катушку (соленоид), который имеет \(N\) витков и длину \(L\). Площади каждого витка – \(S\) (площадь поперечного сечения катушки). Индуктивность такой катушки можно рассчитать по формуле.

$$L = \frac{\mu_0 \cdot N^2 \cdot S}{l}$$

\(\mu_0\ =\ 1.25664\ \cdot\ 10^{-6}\ \frac{N}{A^2}\ -\ Магнитная\ постоянная\)

Расчет индуктивности параллельного и последовательного соединения катушек. Параллельное соединение:

$$\frac{1}{L_{общее}} = \sum_i \frac{1}{L_i}$$

Последовательное соединение:

$$L_{\text{общее}} = \sum_i L_i$$

Энергия магнитного поля в катушке с током.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого током.

$$W = \frac{L I^2}{2}$$

Принцип действия Реле и Генератора.

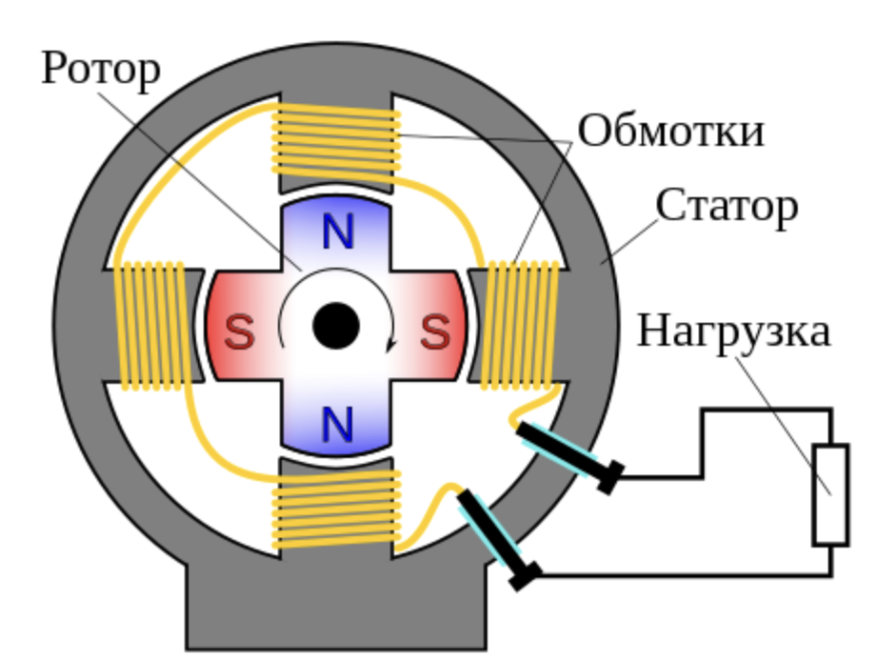
Генератор.

Основные элементы генератора: – Постоянный магнит (Чаще всего – ротор) – Катушки индуктивности (Обмотки) Принцип работы: Вращающийся магнит создает вокруг себя изменяющееся магнитное поле. В обмотках, находящихся в этом изменяющемся поле, наводится индукционный ток.

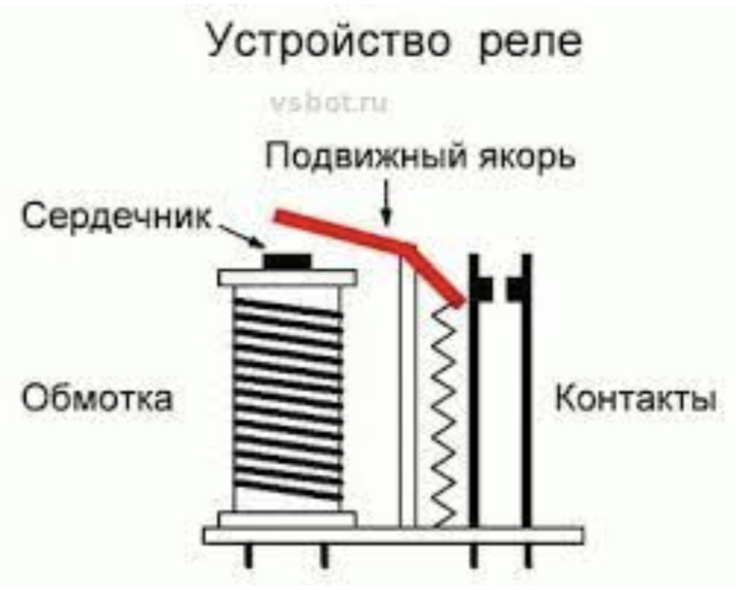
Реле.

Реле используют для замыкания или размыкания электрической цепи, без непосредственного контакта с выключателем. Реле – электромагнитное устройство, включающее или отключающее основную цепь. (Электромагнитный выключатель).

Принцип работы:

При подачи напряжения на реле, электромагнит притягивает подвижный элемент выключателя. Подвижный элемент соединяет контакты, тем самым замыкая цепь. При выключении электромагнита, контакты расходятся и цепь размыкается.

Пример задач.

1. Найдите индуктивность катушки длинной 0.05 \(м\), состоящей из 1000 витков, если её диаметр равен 1 \(см\).

2. Найдите максимальное значение энергии, которое можно запасти в катушке из задачи 1 использованием не идеального источника 5 \(В\) с сопротивлением 20 \(Ом\).

\( Дано: \) \( U = 5 \ В \) \( R = 20 \ Ом \) \( Найти\ W = ? \)

\( Решение: \) \ 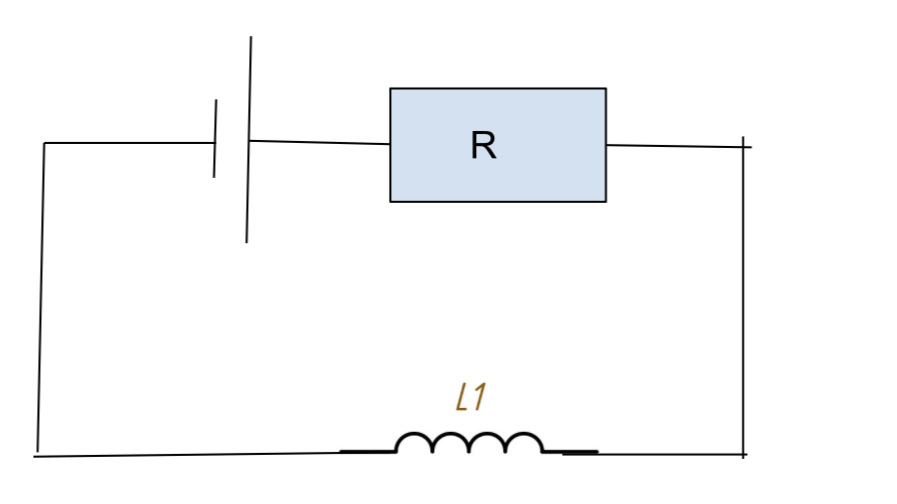Энергия катушки зависит от тока протекающего в ней. Максимальное значение достигается при максимальном токе: $$ I_{max}\ = \frac{U}{R_{цепи}}\ = \frac{U}{R}$$ $$W = \frac{L I^2}{2}\ = \frac{L (\frac{U}{R})^2}{2}\ = \frac{L U^2}{2R^2}$$ Подставим значения: $$W = \frac{0.002 \cdot 5^2}{2 \cdot 20^2}\ = 0,0000625\ Дж $$ \( Ответ:\ W = 0,0000625\ Дж \)