- +7 701 537 76 67
Электромагнитная индукция. Магнитный поток. ЭДС индукции в проводнике, движущемся в магнитном поле. Закон Фарадея.
Основные термины и необходимые понятия:
- Электромагнитной индукция
- Магнитный поток
Магнитный поток.
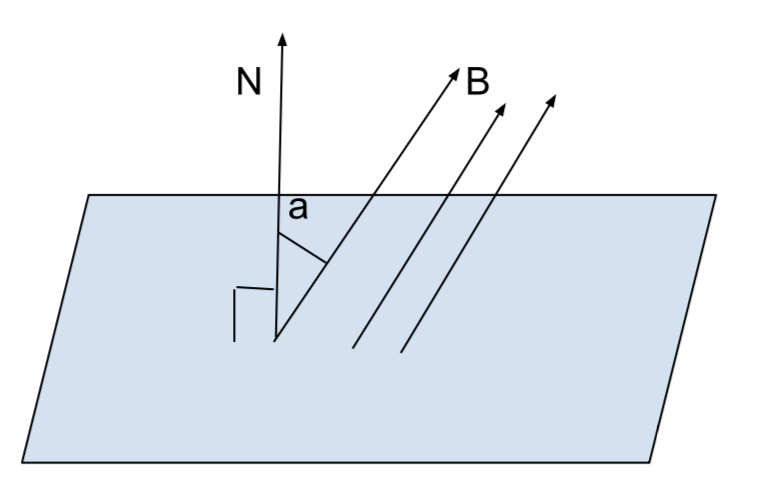
Единица измерения: Вебер. |
Магнитный поток — скалярная величина, равная произведению вектора магнитной индукции на площадь поверхности, которую он пронизывает.$$\Psi = \vec{B} \cdot \vec{S} = B \cdot S \cdot \cos{\alpha}$$ |
ЭДС индукции в проводнике, движущемся в магнитном поле.
Рассмотрим проводник, движущийся в магнитном поле. Внутри проводника есть заряды. (Электроны и ядра атомов) На каждый заряд действует сила Лоренца, так как заряд двигается вместе с проводником в магнитном поле.
$$\vec{F}_\text{л} = q \cdot \vec{V} \times \vec{B}$$
\(Где\ \vec{V}- \ Вектор\ скорости\ ,\vec{B}\ -\ вектор\ магнитной\ индукции. \)
Работа силы Лоренца по перемещению заряда с одного конца проводника на другой против сил электрического взаимодействия зарядов.
$$ A_\text{эл} = A_\text{лор} = \vec{F}_\text{л} \cdot l = q \cdot \vec{V} \times \vec{B} \cdot l $$
\(l\ -\ Длина\ проводника\ и\ расстояние\ на\ которое\ переместился\ q.\)
ЭДС между концами проводника:
$$
E = \frac{A_\text{эл}}{q} = \frac{q \cdot \vec{V} \times \vec{B} \cdot l}{q} = \vec{V} \times \vec{B} \cdot l $$
$$ \downarrow $$
$$
|E| = \left| \frac{q \cdot \vec{V} \times \vec{B} \cdot l}{q} \right| = \frac{q \cdot V \cdot B \cdot l \cdot \sin(\alpha)}{q} = V \cdot B \cdot l \cdot \sin(\alpha)
$$
Закон Фарадея.
Напомним, что для изображения магнитного поля используют силовые (магнитные) линии. Плотность силовых линий показывает силу поля в данной точке пространства.
Закон Фарадея:
Сила индукционного тока в замкнутой цепи прямо пропорциональна быстроте изменения числа силовых (магнитных) линий, которые пронизывают площадь, ограниченную этой цепью.
$$
\mathcal{E} = -\frac{\Delta \Psi}{\Delta t}
$$
\(Где\ \Delta \Psi,\ -\ изменение\ магнитного\ потока\ за\ время\ \Delta t.\)
Рассмотрим рамку с током, в которой один из проводников может двигаться уменьшая или увеличивая площадь рамки.
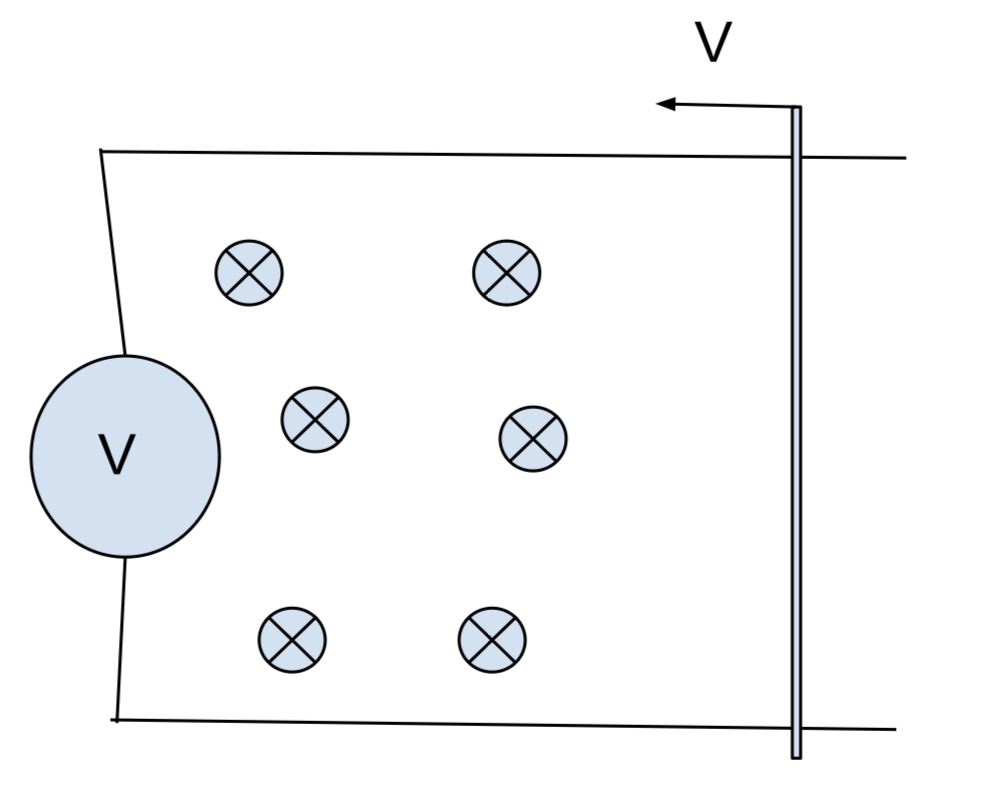
|
$$ \Delta S = -V \cdot l \cdot \Delta t $$ $$Где\ \Delta S,\ -\ изменение\ площади\ рамки\ за\ время\ \Delta t.$$ $$ \Delta \Psi = \Delta (\vec{B} \cdot \vec{S}) = -\vec{S} \cdot \vec{B} = -V \cdot B \cdot l \cdot \Delta t \cdot \cos(\lambda) $$ |
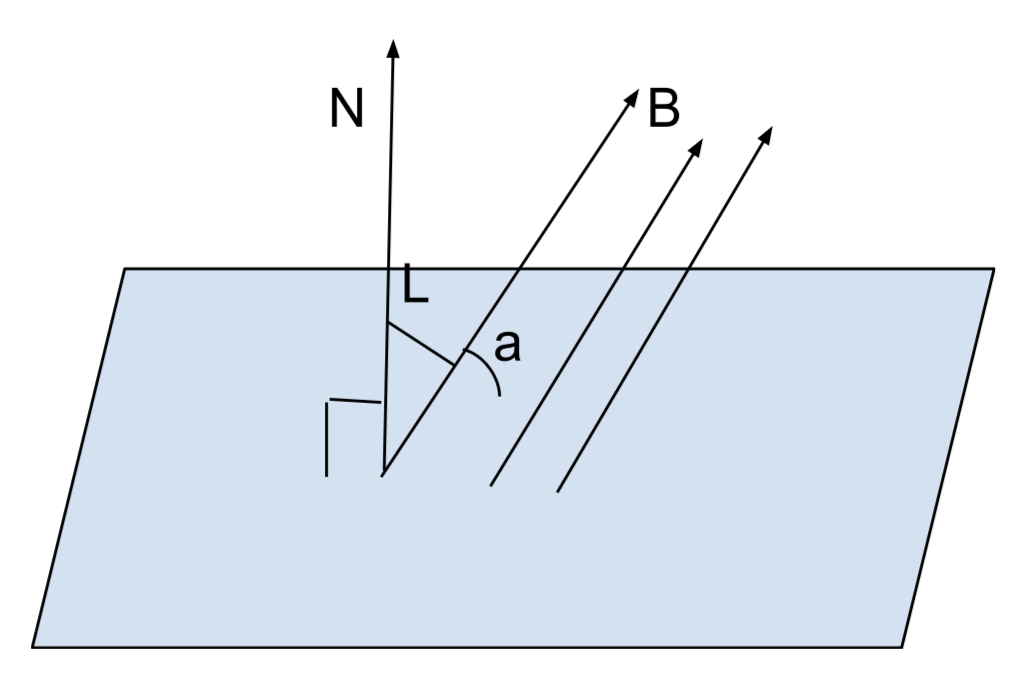
|
\(\lambda\) - угол между (на рисунке \(L\)) перпендикуляром (нормалью) к плоскости рамки и вектором \(\vec{B}\). \(\Rightarrow\) \(\alpha\) = 90 - \(\lambda\) – угол между вектором скорости проводника и вектором \(\vec{B}\). |
По закону электромагнитной индукции:
$$
\Delta \Psi = \Delta (\vec{B} \cdot \vec{S}) = -V \cdot B \cdot l \cdot \Delta t \cdot \cos(90^\circ - \lambda) = -V \cdot B \cdot l \cdot \Delta t \cdot \sin(\alpha)
$$
$$
E = -\frac{\Delta \Psi}{\Delta t} = \frac{V \cdot B \cdot l \cdot \Delta t \cdot \sin(\alpha)}{\Delta t} = V \cdot B \cdot l \cdot \sin(\alpha)
$$
Определение направления тока в рамке:
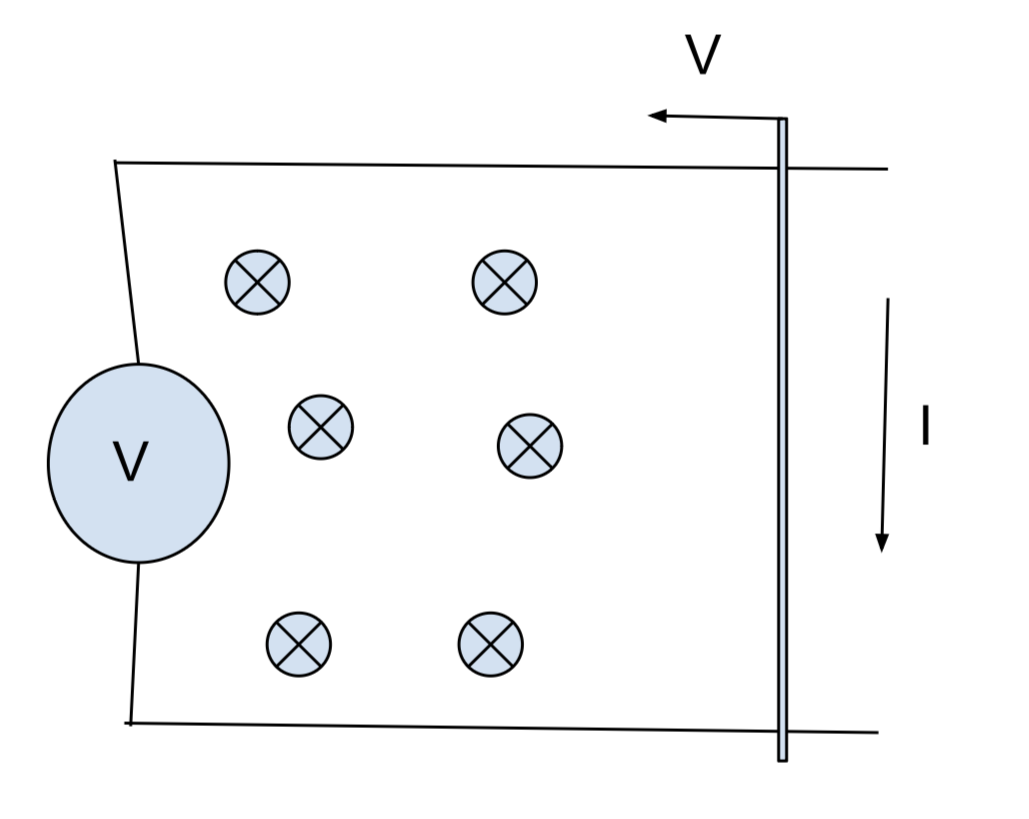
|
Как нам известно:
$$ |
Для определения направления тока в проводнике используется правило правого винта:
(Или что то-же самое левой руки)
|
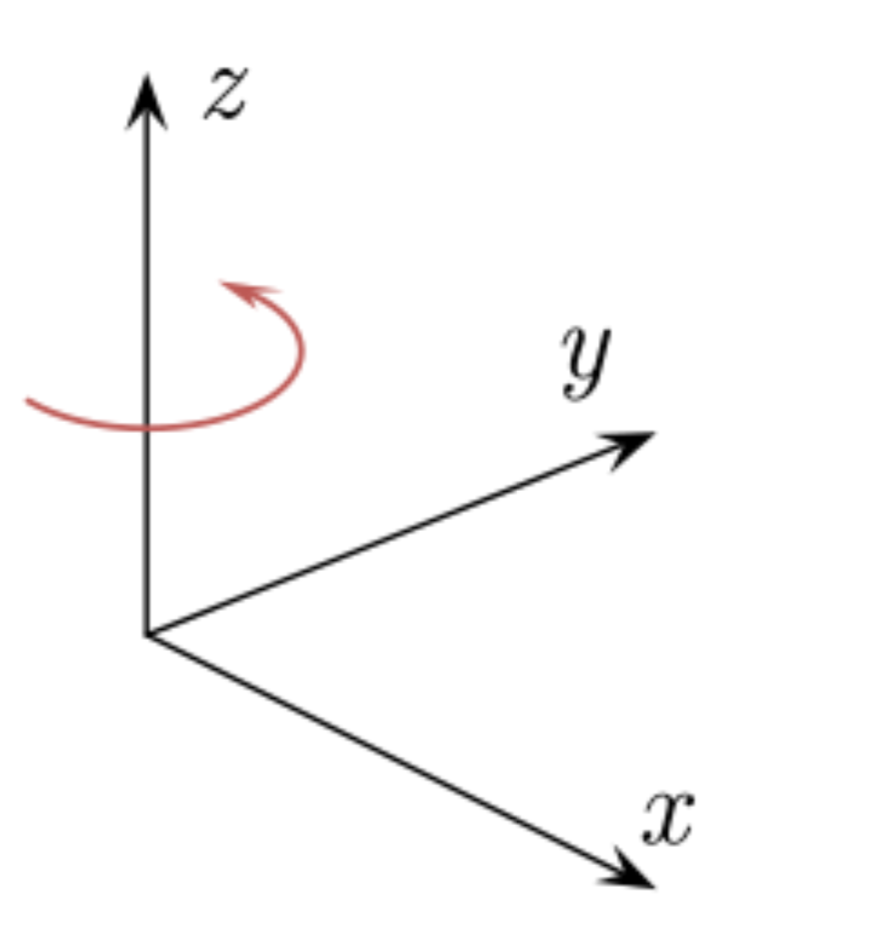
Правило правого винта:
«Если нарисовать векторы так, чтобы их начала совпадали и вращать первый вектор-сомножитель кратчайшим образом ко второму вектору-сомножителю, то буравчик (винт), вращающийся таким же образом, будет ввинчиваться в направлении вектора-произведения». Z – укажет направление тока в проводнике. |
Правило Левой руки:
-
\(\vec{B}\) направлен в ладонь левой руки.
-
4 пальца сонаправлены с \(\vec{V}\).
-
Оттопыренный большой палец указывает направление тока.
Электромагнитная индукция.
Электромагнитной индукция – явление возникновения тока в замкнутой цепи, при изменении магнитного поля, пронизывающего цепь, чаще всего вызывается движением магнита относительно элемента цепи.
Пример эксперимента:
Если вставлять или вынимать магнит из катушки с большим количеством витков, гальванометр будет регистрировать наличие тока, протекающего через катушку.
Ток, возникающий вследствие явления электромагнитной индукции, называют индукционным током.
Самоиндукция.
Электромагнитной индукция – явление возникновения тока в замкнутой цепи, при изменении магнитного поля, пронизывающего цепь, чаще всего вызывается движением.
Пример задач.
1. Рассчитайте магнитный поток через круглую площадку ограниченную проводником, радиус равен 10 \(см\), если вектор магнитной индукции направлен под углом 30 градусов к плоскости площадки и равен 10 \(Тл\).
| \( Дано: \) \( R = 10 \ см = 0{,}10 \ м \) \( B = 10 \ Тл \) \( \alpha = 30^\circ \) \( Найти\ \Psi = ? \) |
\( Решение: \) $$\Psi = \vec{B} \cdot \vec{S} = B \cdot S \cdot \cos{\alpha}$$ Подставим значения: $$\Psi = \vec{B} \cdot \vec{S} = B \cdot \pi R^2 \cdot \cos60^\circ\ =\ 10 \cdot \pi \cdot 0,1^2 \cdot 0,5 = 0.05 \pi = 0.157\ Вебер$$ \( Ответ: \Psi = 0.157 \ Вебер \) |
2. По двум контактам скользит металлический стержень, как показано на рисунке. Определите направление тока в стержне (Вверх или вниз). Найдите силу тока если \(\vec{B}\) = 1 \(Тл\), \(\vec{V}\) = 10 \(м/c\), общее сопротивление проводников \(R\) = 10 \(Ом\), длина проводника 1 \(м\).
| \( Дано: \) \( \vec{B} = 1 \ Тл \) \( \vec{V} = 10 \ м/с \) \( R = 10 \ Ом \) \( l = 1 \ м \) \( Найти\ I = ? \) |
\( Решение: \)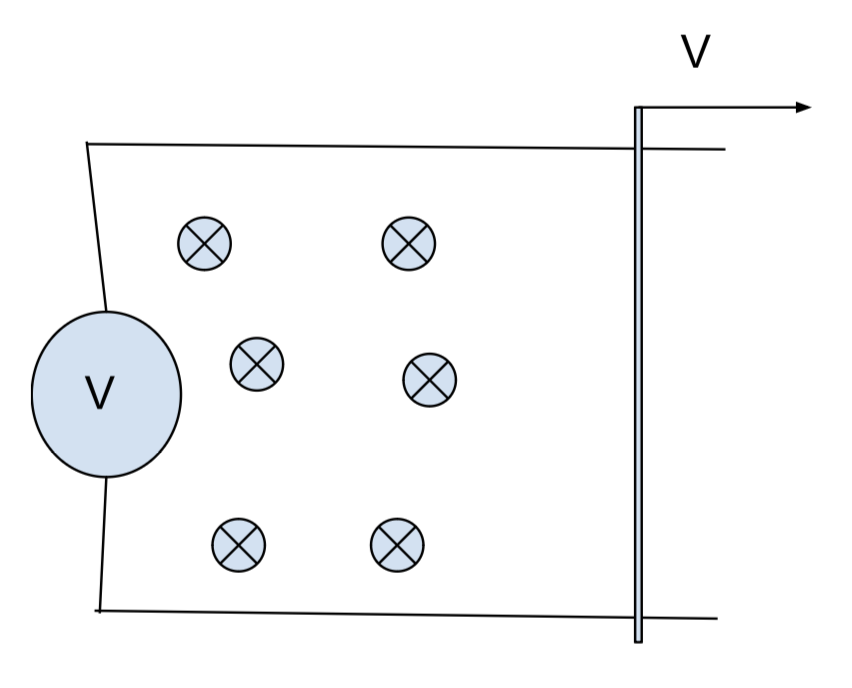
$$ По закону Ома: $$ I\ = \frac{E}{R}\ = \frac{V \cdot B \cdot l \cdot \sin(\alpha)}{R}$$ Подставим значения: $$ I\ = \frac{1 \cdot 10 \cdot 1 \cdot \sin(90)}{10}\ = 1\ А$$ \( Ответ:\ I = 1\ А \) |
3. Для условий задачи №2, найдите силу, которую нужно прикладывать к стержню, чтобы он двигался равномерно и прямолинейно со скоростью \(\vec{V}\).
| \( Дано: \) \( \vec{B} = 1 \ Тл \) \( \vec{V} = 10 \ м/с \) \( R = 10 \ Ом \) \( l = 1 \ м \) \( Найти\ F_{внеш} = ? \) |
\( Решение: \) Определим, какие силы сопротивления действуют на стержень. Как было определено выше, перед нами стержень с током, двигающийся в магнитном поле. На такой стержень действует сила Ампера, которую мы должны компенсировать внешним воздействием. $$F_{внеш}\ =\ F_А\ =\ \vec{I} \cdot \vec{B} \cdot l\ = I \cdot B \cdot l \cdot \sin(\alpha)$$ Подставим значения: $$F_{внеш}\ = 1 \cdot 1 \cdot 1 \cdot \sin(90)\ =\ 1\ Н$$ \( Ответ:\ F_{внеш} = 1\ Н \) |