Ток. Напряжение. Сопротивление.

Электрический ток — направленное движение заряженных частиц (электронов или ионов) под действием электрического поля.

Условия существования тока:

• наличие свободных зарядов (например, в металле — электроны);
• наличие электрического поля (источник тока);
• замкнутая электрическая цепь.

Электрические цепи и параметры участков цепи.

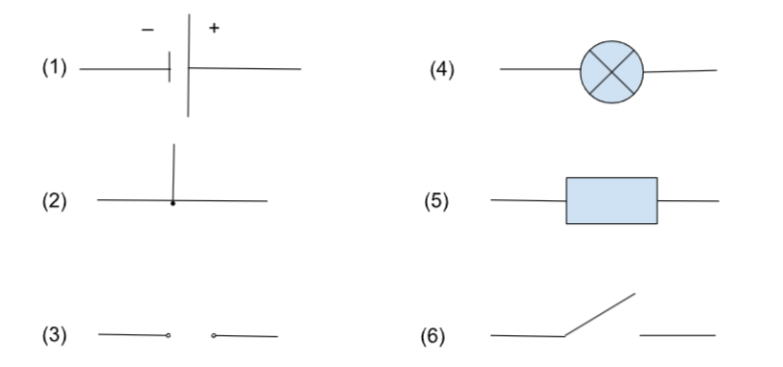
1. Источник тока, источник Электродвижущей силы (ЭДС), Гальванический элемент или аккумулятор/батарейка.
2. Проводники и соединение проводников
3. Разрыв в цепи или место для подключения прибора
4. Лампа
5. Резистор/элемент обладающий электрическим сопротивлением.
6. Ключ/выключатель – элемент, который может менять состояние: разрыв в цепи или проводник.

Сила тока \(I\)-физическая величина, равная отношению заряда прошедшего через поперечное сечение проводника за время t, к этому времени t.

$$ I = \frac{q}{t}\ $$ где:

• \( I — сила \ тока \ [А]\),
• \( q — заряд,\ прошедший \ через \ сечение \ проводника \ [Кл]\),
• \( t — время \ [с]\).

Напряжение \(U\) численно равно работе электрического поля при перемещении единичного положительного заряда вдоль силовых линий поля.

$$ U=\Delta \phi =\frac{A}{q}$$ где:

• \(A - работа \ [Дж] \),
• \(q - заряд \ [Кл] \).

Отношение напряжения U между концами участка цепи (проводника) к силе тока в нем называют сопротивлением \(R\) этого участка цепи (проводника). $$ R=\frac{U}{I}$$

Удельное сопротивление — величина, характеризующая способность проводника препятствовать прохождению тока.

Зависит от:

$$ R = \rho \cdot \frac{l}{S} $$

где:

• \( R — сопротивление \ [Ом]\),
• \( \rho — удельное \ сопротивление \ [Ом·м]\),
• \( l — длина \ проводника \ [м]\),
• \( S — площадь \ поперечного \ сечения \ [м²]\).

Закон Ома для участка цепи

$$ I = \frac{U}{R} $$

где:

• \( I — сила \ тока \ [А]\),
• \( U — напряжение \ на \ участке \ цепи \ [В]\),
• \( R — сопротивление \ [Ом]\).

Соединения проводников

Тип соединения	Сопротивление	Ток	Напряжение	Схема
Последовательное	\( R = R_1 + R_2 + \ldots \)	\( I = I_1 = I_2 = \ldots \)	\( U = U_1 + U_2 + \ldots \)
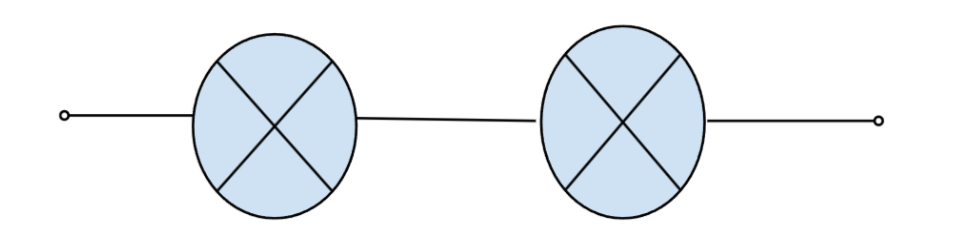
Параллельное	\( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots \)	\( I = I_1 + I_2 + \ldots \)	\( U = U_1 = U_2 = \ldots \)

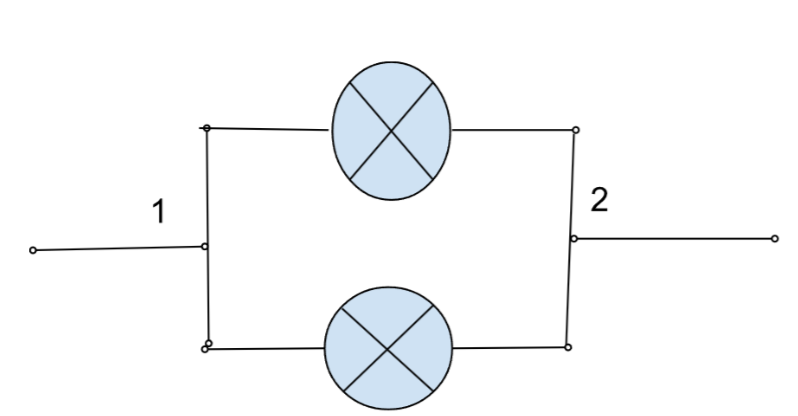
Схемы подключения приборов

• Амперметр — подключается последовательно, измеряет силу тока.
• Вольтметр — подключается параллельно, измеряет напряжение.

Пример задач

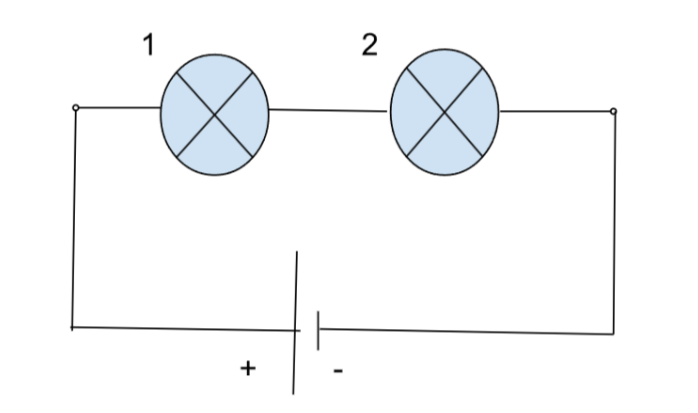
1.В приведенной ниже схеме сопротивление ламп равно \(R_1\)=300 Ом,\(R_2\)=200 Ом. Напряжение, создаваемое источником тока, равно 5В. Найти силу тока в цепи.

Дано: \( R_1 = 300\ Ом \) \( R_2 = 200\ Ом \) \( U = 5\ \text{В} \) Найти: \( I = ? \)

Решение: Предположим, что резисторы соединены последовательно. Тогда общее сопротивление: $$ R = R_1 + R_2 = 300 + 200 = 500\ \text{Ом} $$ Закон Ома: $$ I = \frac{U}{R} = \frac{5}{500} = 0.01\ \text{А} $$ Ответ: \( I = 0.01\ \text{А} \)

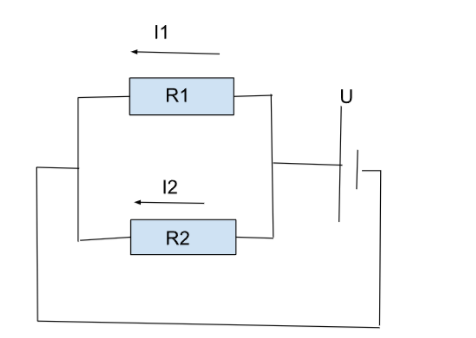
2.Два параллельно соединенных резистора подключены к источнику тока. Найдите как соотношение токов, проходящих через соответствующие резисторы, зависит от сопротивлений \(R_1,R_2\). Найдите \(I_1,I_2\), если известно, что \(R_1\)=20 Ом,\(R_2\)=25 Ом, U=5 В.

Дано: \( R_1 = 20\ Ом \) \( R_2 = 25\ Ом \) \( U = 5\ \text{В} \) Найти: \( I_1,\ I_2,\ \frac{I_1}{I_2} \)

Решение: Напряжение на каждом резисторе одинаково (параллельное соединение): $$ I_1 = \frac{U}{R_1} = \frac{5}{20} = 0.25\ \text{А} $$ $$ I_2 = \frac{U}{R_2} = \frac{5}{25} = 0.2\ \text{А} $$ Соотношение токов: $$ \frac{I_1}{I_2} = \frac{0.25}{0.2} = 1.25 $$ Или через сопротивления: $$ \frac{I_1}{I_2} = \frac{R_2}{R_1} = \frac{25}{20} = 1.25 $$ Ответ: \( I_1 = 0.25\ \text{А},\ I_2 = 0.2\ \text{А},\ \frac{I_1}{I_2} = 1.25 \)

3.В схеме состоящей из 2-х ламп и источников тока, соединенных параллельно \(R_1\)=100 Ом. Напряжение, создаваемое источником тока, равно 5В. При этом сила тока в цепи через источник равна 0.09 А. Найдите сопротивление второй лампы.