Постоянный ток: законы, работа и эффективность

Закон Ома для полной цепи-сила тока полной цепи пропорциональна ЭДС и обратно пропорциональна полному сопротивлению цепи:

$$ I = \frac{U}{R + r} $$

где:

• \(I — сила \ тока \ в \ цепи \ (через \ источник, \ если \ не \ оговорено \ другое)\),
• \(U — напряжение \ источника \ тока\),
• \(R — общее \ сопротивление \ резисторов, \ ламп, \ приборов \ в \ цепи\),
• \(r — собственное \ сопротивление \ источника \ тока.\)

Короткое замыкание — это состояние электрической цепи, при котором ток проходит по недопустимому маршруту, на котором обычно практически отсутствует (или очень низкое) электрическое сопротивление.

Если напряжение между концами участка цепи равно \(U\), то при прохождении заряда \(q\) через этот участок электрическое поле совершает работу:

$$ A = Uq $$

Или, используя силу тока \(I\) и время \(t\):

$$ A = UIt $$

Закон Джоуля — Ленца - тепловая энергия \(Q\), выделяемая в проводнике при прохождении тока, рассчитывается по формуле:

$$ Q = I^2 R t $$

Мощность тока в цепи:

$$ P = UI $$

По определению КПД:

$$ \eta = \frac{A_{\text{полезная}}}{A_{\text{общая}}} = \frac{R_{\text{цепи}}}{R_{\text{цепи}} + r_{\text{источника}}} $$

Пример задач

1.Какую работу совершит зарядное устройство мобильного телефона за 4 часа зарядки, если напряжение на клеммах равно 1.5 \(В\), а сила тока равна 0.25 \(А\).

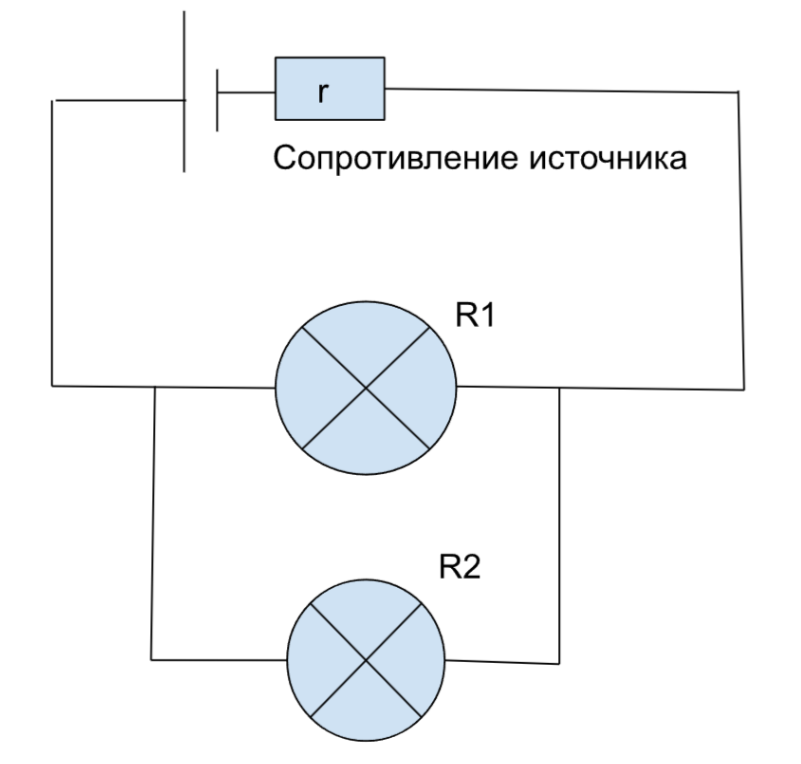
2.К не идеальному источнику тока подключили 2 лампы параллельно друг другу. Найти энергию, выделившуюся на второй лампе за 1 минуту, если сопротивления ламп и источника равны соответственно: \(R_1\)=20 Oм \(R_2\)=5 Oм \(r\)=1 Oм. Напряжение на клеммах источника равно 10 \(В\).

\( Дано:\) \( U = 10\,В \) \( R_1 = 20\,\text{Ом} \), \( R_2 = 5\,\text{Ом} \), \( r = 1\,\text{Ом} \) \( t = 1\, \text{мин} = 60\,\text{с} \) \( Найти: E_{R2} = ? \)

\( Решение:\) Лампы подключены параллельно, значит напряжение на лампах одинаковое. Но сначала нужно найти ток в цепи и напряжение на второй лампе. Сначала найдём общее сопротивление двух ламп в параллели: \[ R_{\text{паралл}} = \frac{R_1 R_2}{R_1 + R_2} = \frac{20 \times 5}{20 + 5} = \frac{100}{25} = 4\,\text{Ом} \] Общее сопротивление цепи: \[ R_{\text{общ}} = r + R_{\text{паралл}} = 1 + 4 = 5\,\text{Ом} \] Сила тока в цепи: \[ I = \frac{U}{R_{\text{общ}}} = \frac{10}{5} = 2\,\text{А} \] Напряжение на параллельном соединении ламп: \[ U_{\text{ламп}} = I \times R_{\text{паралл}} = 2 \times 4 = 8\,В \] Ток через вторую лампу: \[ I_2 = \frac{U_{\text{ламп}}}{R_2} = \frac{8}{5} = 1.6\,\text{А} \] Энергия, выделившаяся на второй лампе за 60 секунд: \[ E_{R2} = U_{\text{ламп}} \times I_2 \times t = 8 \times 1.6 \times 60 = 768\,\text{Дж} \] \( Ответ: E_{R2} = 768\,\text{Дж} \)

3.Через нагревательный элемент сопротивлением 100 Oм, проходит ток 6 \(А\). При этом этот нагреватель доводит 5 литра воды от 25 градусов до кипения за 10 минуту. Найдите КПД нагревательного прибора.