Электрический ток в металлах.

Основные термины:

• Электрический ток
• Свободные электроны
• Электронная проводимость
• Модель "электронный газ"
• Закон Ома
• Сопротивление
• Кристаллическая решетка
• Закон Джоуля-Ленца

Электрический ток - Материал, обладающий свободными электронами, способными передавать электрический ток. Электрический ток в металлах обусловлен движением свободных электронов, которые под воздействием внешнего электрического поля двигаются в определенном направлении, что приводит к образованию электрического тока.

Свободные электроны - электроны в металле, которые свободно движутся под воздействием электрического поля.

Ион - заряженная частица, образованная атомом, который приобрел заряд вследствие потери или приобретения одного или нескольких электронов.

Электронная проводимость - способность металлов и других материалов передавать электрический ток через свободные электроны.

Удельный заряд - отношение заряда частицы к её массе, выраженное в кулон/килограмм, что является мерой взаимодействия частицы с электрическим и магнитным полями.

Закон Ома - математическое выражение, устанавливающее линейную зависимость между напряжением, силой тока и сопротивлением в электрической цепи: \( I = \frac{U}{R} \)

Сопротивление - мера того, как материал затрудняет прохождение электрического тока через него.

Кристаллическая решетка - регулярное трехмерное расположение атомов или ионов в кристаллическом веществе. В случае металлов, это важно для понимания передвижения свободных электронов.

Инерция носителей заряда - свойство заряженных частиц сохранять свою скорость и направление движения, пока на них не действует внешняя сила.

Промежуток времени \(t\) - среднее время между двумя последовательными столкновениями электрона с ионами кристаллической решетки.

рис.1.0 - упорядоченное движение свободных электронов в поле

Вещества, обладающие электронной проводимостью, называют проводниками первого рода. Металлический проводник можно рассматривать как физическую систему, состоящую из свободных электронов и положительно заряженных ионов, колеблющихся около положений равновесия.

Модель "электронный газ" - упрощенное представление о свободных электронах в металле, которые движутся по кристаллической решетке, подобно частицам в идеальном газе.

При формировании металлического кристалла из нейтральных атомов, электроны, находящиеся на внешних оболочках атомов, становятся слабо связанными со своими ядрами. Этот процесс происходит, когда атомы сближаются в кристаллической структуре на расстояние порядка 0,1 нм. В результате электроны начинают взаимодействовать не только со своими ядрами, но и с ядрами соседних атомов, что приводит к ослаблению связи с собственными ядрами. Таким образом, они приобретают свободу перемещения по всему кристаллу, что аналогично движению частиц идеального газа. В результате этого процесса образуется модель "электронного газа", которая описывает движение свободных электронов в кристаллической решетке металла.

рис.2.0 — свободные электроны и положительно заряженные ионы.

В модели "электронного газа" электроны рассматриваются как материальные точки, движущиеся под воздействием электрического поля. Их движение описывается законами классической механики, где столкновения с ионами кристаллической решётки считаются неупругими. В промежутках между столкновениями электроны совершают беспорядочное тепловое движение, но при этом под воздействием электрического поля движутся упорядоченно и равноускоренно.

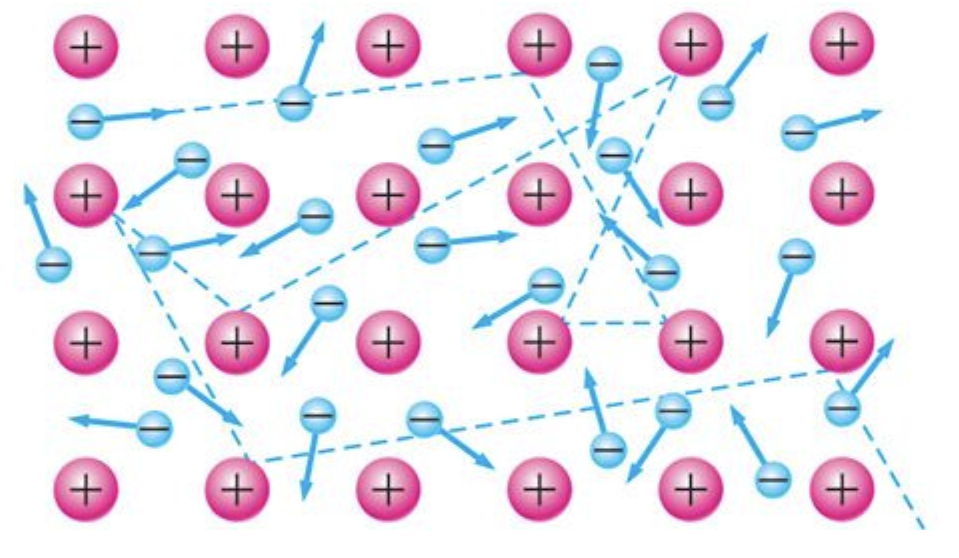
рис.3.0 — движение одного из электронов

Модель электронного газа позволяет теоретически объяснить природу сопротивления и обосновать закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов.

Пусть электрон движется с ускорением в направлении, противоположном направлению напряженности электрического поля, тогда: $$\vec{a} = \frac{\vec{F}}{m_0} = -\frac{e\vec{E}}{m_0}$$

рис.4.0 — движение электрона

\(m_{0}\ -\ масса\ электрона,\ e\ -\ модуль\ заряда\ электрона\)

Тогда модуль средней скорости его направленного движения: $$\vec{v} = \frac{a \vec{t}}{2} = \frac{eE \vec{t}}{2 m_0}$$

\(\vec{t}\) - усредненный промежуток времени между двумя последовательными столкновениями электрона с ионами кристаллической решётки.

Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряженности этого поля.

$$E = \frac{U}{l}$$

\(где\ l\ —\ длина\ проводника,\ U\ —\ напряжение\ между\ его\ концами.\)

Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника

$$\vec{v} = \frac{eU \vec{t}}{2 m_0 l} \sim U$$

Сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:

$$I = \frac{q}{t} = \frac{eN}{t} = \frac{eN \vec{v}}{l} = \frac{enV \vec{v}}{l} = en \vec{v} S$$

\(где\ q\ —\ модуль\ заряда\ электронов\ проводимости,\ находящихся\ в\ проводнике\) $$t = \frac{l}{\vec{v}}$$ — усреднённое время прохождения этих электронов по проводнику, \(N\) — количество электронов проводимости в проводнике, \(n\) электронов, \(V = Sl\) — объём проводника. Следовательно, сила тока пропорциональна напряжению между концами проводника — концентрация этих \( I \sim U \).

Зависимость сопротивления металлов от температуры.

$$R = \rho \frac{l}{S}$$ сопротивление зависит от рода вещества (удельного сопротивления \(ρ\)) и их геометрических размеров (длины \(l\) и площади поперечного сечения \(S\)).

Удельное сопротивление вещества металлического проводника зависит от концентрации свободных носителей заряда и частоты их столкновений с ионами кристаллической решётки, совершающими колебательные движения около положений устойчивого равновесия.

В металлических проводниках концентрация свободных электронов практически постоянна для данного проводника и не зависит от температуры. Однако частота столкновений свободных электронов с ионами кристаллической решётки с ростом температуры возрастает. Это приводит к возрастанию удельного сопротивления металлического проводника при повышении температуры.

При описании температурной зависимости удельного сопротивления проводника вводят температурный коэффициент сопротивления \(α\), численно равный относительному изменению удельного сопротивления вещества проводника при приращении его температуры на \(1\ К\): $$\alpha = \frac{\rho - \rho_0}{\rho_0 (T - T_0)}$$ где \( \rho_0 \) и \( \rho \) — удельные сопротивления вещества проводника соответственно при температуре \( T_0 = 273\ К \) (0 °C) и данной температуре \( T \).

Из формулы следует, что \( \rho = \rho_0 (1 + \alpha \Delta T) \), где \( \Delta T = T - T_0 \) — приращение абсолютной температуры проводника, которое совпадает с приращением температуры по шкале Цельсия (\( \Delta T = \Delta t \)). Таким образом, удельное сопротивление вещества металлического проводника возрастает с увеличением температуры.

Поскольку сопротивление проводника \( R = \rho \dfrac{l}{S} \) то, пренебрегая незначительной температурной зависимостью отношения \( \dfrac{l}{S} \), можно записать:

\( R = R_0 (1 + \alpha \Delta T) = R_0 (1 + \alpha \Delta t) \), где \( R_0 \) и \( R \) — сопротивления проводника соответственно при температуре \( T_0 = 273\,\text{K} \) (0 °C) и данной температуре \( T(t) \).

Для металлических проводников эти формулы применимы при температурах \( T > 140\ К \). У всех металлов при повышении температуры сопротивление возрастает, т. е. температурный коэффициент сопротивления \( \alpha \) — величина положительная.

Для большинства металлов (но не сплавов) при температурах от 0 до 100 °C среднее значение температурного коэффициента сопротивления: \[\langle \alpha \rangle \approx \frac{1}{273}\ K^{-1}\]

Сверхпроводимость.

Температуру, при которой электрическое сопротивление проводника уменьшается до нуля, называют критической температурой. Состояние проводника при этом называют сверхпроводимостью, а сам проводник — сверхпроводником. Каждый сверхпроводящий металл характеризуется своей критической температурой. Явление сверхпроводимости свойственно не только некоторым металлам, но и сплавам, полупроводникам и полимерам.

Если в сверхпроводнике создать электрический ток, то он будет существовать в нём неограниченно долго. При этом для поддержания тока нет необходимости в источнике тока. Это указывает на перспективу использования явления сверхпроводимости при передаче электрической энергии.

Сверхпроводящие соединения нашли применение в качестве материала обмоток электромагнитов для создания сильных магнитных полей в мощных электрических двигателях, генераторах, ускорителях и др. Разрабатывают проекты сверхпроводящих электронно-вычислительных машин. Уже созданы компактные интегральные схемы на сверхпроводниках, обладающие рядом преимуществ по сравнению с имеющимися аналогами.

Пример задач.

1. Определите сопротивление алюминиевого проводника при температуре \( t_2 = 90^\circ\text{C} \), если при температуре \( t_1 = 20^\circ\text{C} \) его сопротивление \( R_1 = 4{,}0\ Ом \). Температурный коэффициент сопротивления алюминия \( \alpha = 4{,}2 \cdot 10^{-3}\ К^{-1} \).