• +7 777 150 51 51

Явление тяготения. Сила тяжести. Вес тела. Невесомость и перегрузка

Основные термины

Закон всемирного тяготения

Закон всемирного тяготения гласит, что каждое тело притягивается к остальным телам с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
$$ F = G \frac{m_1 m_2}{R^2} $$
где \( m_1, m_2 \) — массы тел, \( R \) — расстояние между центрами масс тел, \( G = 6.67 \cdot 10^{-11} \ \text{Н} \cdot \text{м}^2/\text{кг}^2 \) — гравитационная постоянная.

Сила тяжести

Сила тяжести — это сила, с которой Земля (или другое небесное тело) притягивает к себе тела. На поверхности Земли:
$$ F_T = m g $$
где \( g = 9.8 \ \text{м/с}^2 \).

Вес тела, находящегося на опоре или подвесе, равен силе тяжести:
$$ P = m g $$

Ускорение свободного падения

Ускорение свободного падения \( g \) зависит от массы объекта (например, планеты) и расстояния до его центра. На поверхности Земли \( g \approx 9.81 \ \text{м/с}^2 \). На Луне \( g \approx 1.62 \ \text{м/с}^2 \), так как масса Луны меньше массы Земли.

Вес тела

Вес тела — это сила, с которой тело действует на опору или подвес под воздействием силы тяжести. Если тело покоится или движется равномерно:
$$ P = m g $$
При ускорении (например, в лифте):

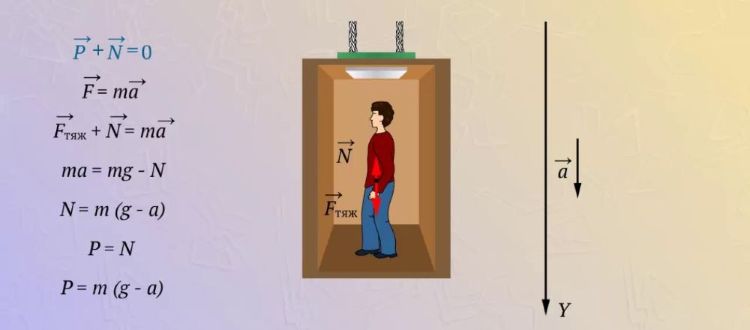
Невесомость

Невесомость возникает, когда объект Невесомость-физическое состояние, при котором объект или человек кажется свободным от воздействия силы тяжести. Невесомость может возникнуть в условиях микрогравитации, например, на орбите вокруг Земли, когда объект находится в свободном падении и не оказывается под действием силы тяжести в полной мере. Если тело движется вниз по вертикали, получаем

$$ m g - N = -m a \implies m g - N = m a \implies N = g (m - a) \implies P = m (g - a) $$

т.е. вес при движении по вертикали с ускорением будет меньше силы тяжести.

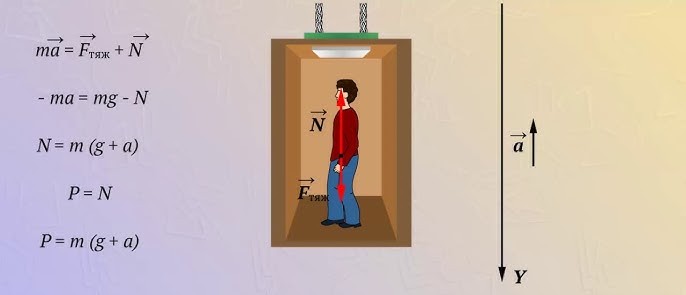
"Схема лифта с телом массой \( m \), где \( m g \) — сила тяжести, \( N \) — нормальная реакция, \( a \) — ускорение лифта, и \( P = m (g - a) \) — вес тела."

Перегрузка

Перегрузка (или гравитационная перегрузка) - это физическое воздействие, при котором организм или объект подвергается ускорению, превышающему ускорение свободного падения на поверхности Земли \( g \approx 9.81 \ \text{м/с}^2 \). В случае движения тела вертикально вверх вместе с опорой с ускорением по второму закону Ньютона можно записать:

В случае движения тела вертикально вверх вместе с опорой с ускорением по второму закону Ньютона можно записать:

$$ m g + N = m a \implies -m a = m g - N \implies N = m (g + a) \implies P = m (g + a) $$

при движении вертикально вверх с ускорением вес тела увеличивается.

"Схема лифта с телом массой \( m \), где \( m g \) — сила тяжести, \( N \) — нормальная реакция, \( a \) — ускорение лифта, и \( P = m (g + a) \) — вес тела."

Примеры решения задач

1. Найдите силу притяжения между Землей и Луной, если масса Земли 6·10²⁴ кг, а масса Луны 7.3·10²² кг, расстояние между ними 3.8·10⁸ м.

\( Дано: \)
\( m_1 = 6 \cdot 10^{24} \ \text{кг} \)
\( m_2 = 7.3 \cdot 10^{22} \ \text{кг} \)
\( R = 3.8 \cdot 10^8 \ \text{м} \)
\( G = 6.67 \cdot 10^{-11} \ \text{Н} \cdot \text{м}^2/\text{кг}^2 \)

\( Найти: F = ? \) 		\( Решение: \)
Используем формулу закона всемирного тяготения:
$$ F = G \frac{m_1 m_2}{R^2} $$
Подставляем значения:
$$ F = 6.67 \cdot 10^{-11} \cdot \frac{(6 \cdot 10^{24}) \cdot (7.3 \cdot 10^{22})}{(3.8 \cdot 10^8)^2} $$
Вычисляем:
$$ F = 6.67 \cdot 10^{-11} \cdot \frac{6 \cdot 7.3 \cdot 10^{24+22}}{(3.8)^2 \cdot 10^{16}} = 6.67 \cdot 10^{-11} \cdot \frac{43.8 \cdot 10^{46}}{14.44 \cdot 10^{16}} = 6.67 \cdot 3.03 \cdot 10^{19} \approx 2 \cdot 10^{20} \ \text{Н} $$
\( Ответ: F = 2 \cdot 10^{20} \ \text{Н} \)

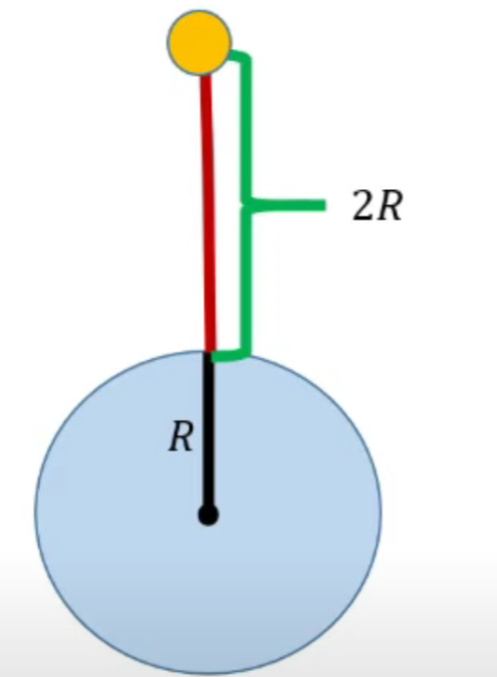
2. Чему равно ускорение свободного падения на высоте над поверхностью Земли, равной её радиусу?

\( Дано: \)
\( h = 2R \)
\( g = 9.8 \ \text{м/с}^2 \)

\( Найти: g = ? \)
\( Решение: \)
Ускорение свободного падения на высоте \( h \) определяется формулой:
$$ g = G \frac{M}{r^2} $$
На поверхности Земли \( r = R \), и \( g = G \frac{M}{R^2} = 9.8 \ \text{м/с}^2 \).
На высоте \( h = 2R \) расстояние от центра Земли \( r = R + h = R + 2R = 3R \). Тогда:
$$ g_h = G \frac{M}{(3R)^2} = G \frac{M}{9R^2} = \frac{1}{9} \cdot G \frac{M}{R^2} = \frac{g}{9} $$
Подставляем \( g = 9.8 \ \text{м/с}^2 \):
$$ g_h = \frac{9.8}{9} \approx 1.09 \ \text{м/с}^2 $$
\( Ответ: g \approx 1.09 \ \text{м/с}^2 \) 		Diagram of Earth with height h equal to radius R

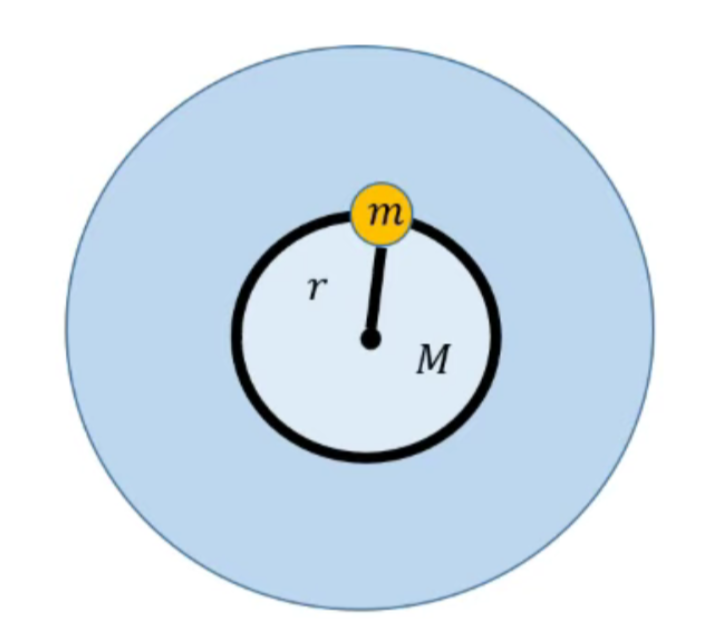
3.С какой силой притягивается к центру Земли тело массой m, находящееся в глубокой шахте, если расстояние от центра Земли до тела равно r? Плотность Земли считайте всюду одинаковой и равной ρ.

\( Дано:\)
\( r \)
\( m \)
\( \rho \)
\( Найти: F = ? \)
\( Решение:\)
Согласно ЗВТ, тело массой \( m \), находящееся не на поверхности планеты, а в глубине шахты, взаимодействует уже не со всей планетой, а только с той её частью (шаром), радиус которой равен расстоянию \( r \) от центра.
Плотность планеты:
$$ \rho = \frac{M}{V} \Rightarrow M = \rho V = \rho \cdot \frac{4}{3} \pi r^3 $$
Тогда сила гравитационного притяжения: $$ F = G \frac{Mm}{r^2} = G \cdot \frac{\rho \cdot \frac{4}{3} \pi r^3 \cdot m}{r^2} = G m \rho \cdot \frac{4}{3} \pi r $$
\( Ответ: F = G m \rho \cdot \frac{4}{3} \pi r \) 		Diagram of Earth with depth r