Сила Архимеда

Основные термины:

Архимедова сила
Гидростатическое давление
Закон Архимеда
Условия плавания

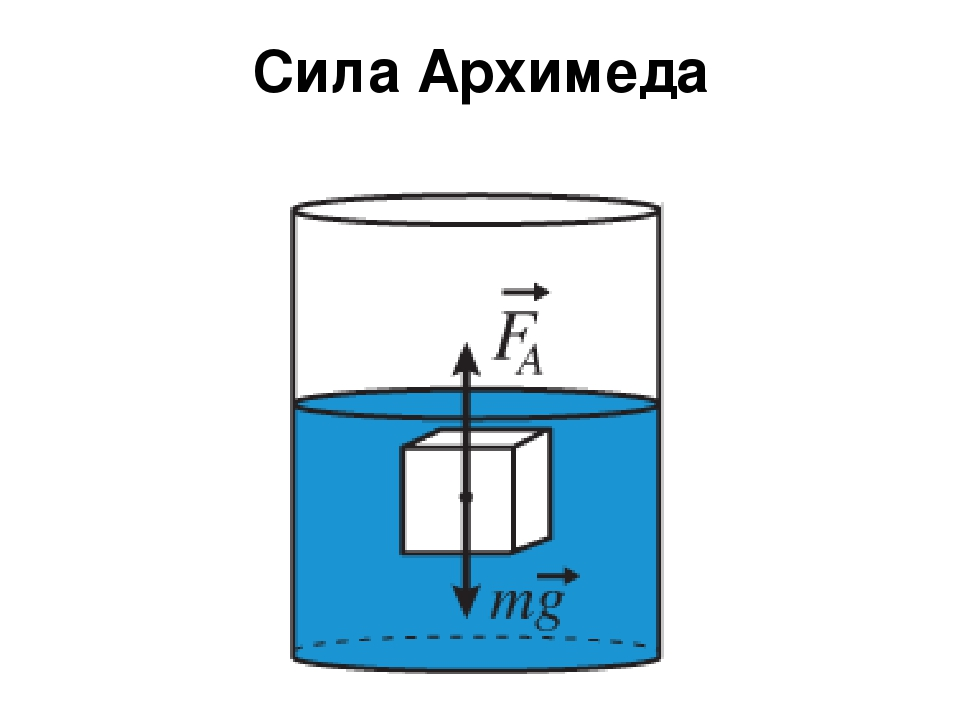
Архимедова сила - cила, действующая на тело, погруженное в жидкость или газ, направленная вверх и равная по модулю весу вытесненной телом жидкости $$F_A = \rho g V$$ где: $ \rho $ — плотность жидкости
$ g $ — ускорение свободного падения
$ V $ — объем вытесненной жидкости

Гидростатическое давление - давление, создаваемое жидкостью в результате её веса, увеличивается с глубиной. $$p = \rho g h \quad [\text{Па}]$$
Закон Архимеда На всякое тело, погруженное в жидкость, действует со стороны этой жидкости поддерживающая сила, равная весу вытесненной телом жидкости. $$F_A = F_2 - F_1 = \rho g (h_2 - h_1) S = \rho g V $$ где:

$ h_1, h_2 $ — глубины погружения нижней и верхней точек тела
$ S $ — площадь основания
$ V $ — объем вытесненной жидкости

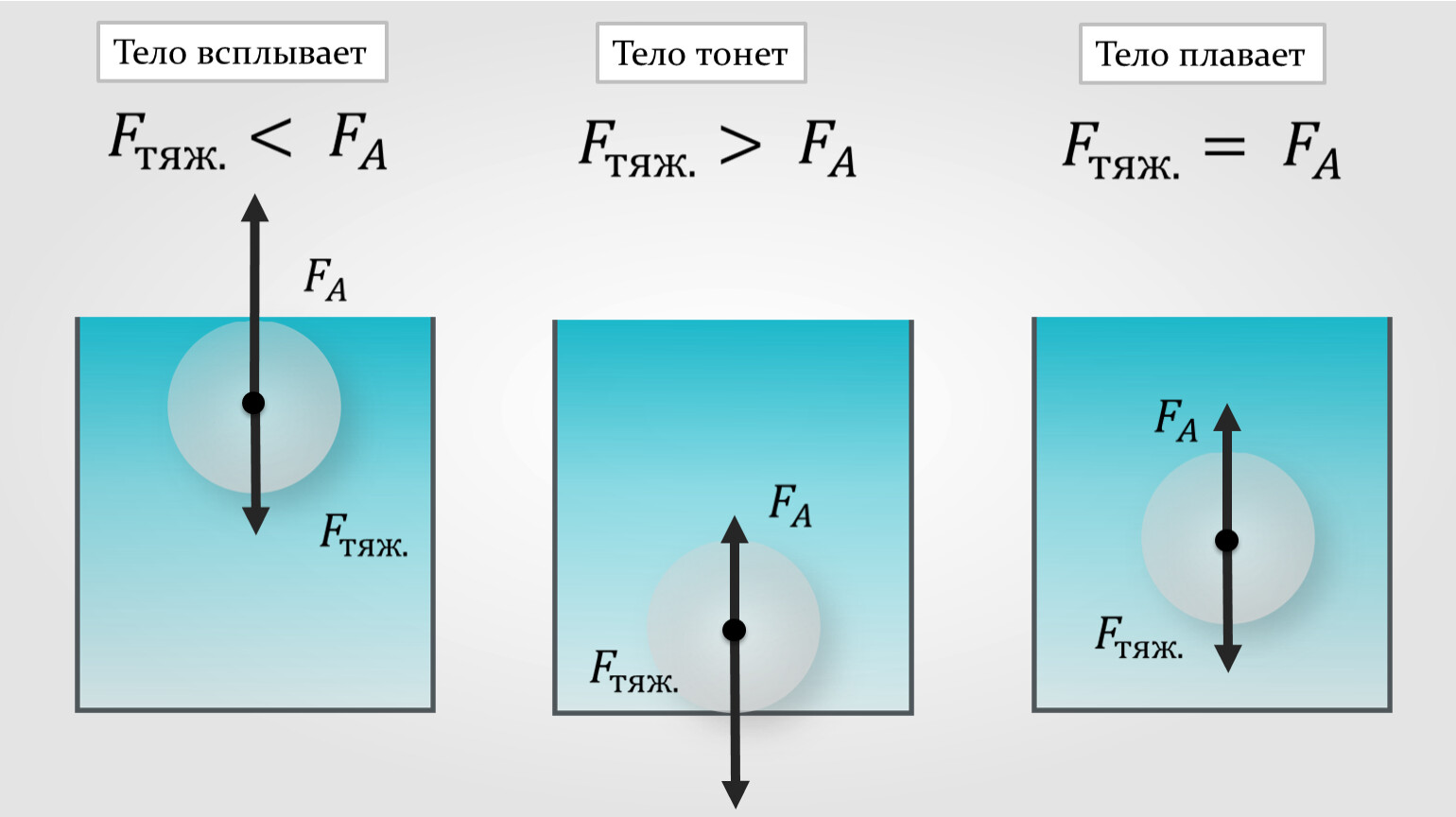
Условия плавания тела в жидкости:

Тело всплывает, если $ F_A > mg $
Тело плавает, если $ F_A = mg $
Тело тонет, если $ F_A < mg $

Примеры решения задач

1.Какой должна быть площадь плоской длины толщиной 40 см, чтобы удержать на воде груз массой 100 кг? Глубина погружения длины должна быть равна 38 см.

$ Дано: $
$ h = 0{,}4 \ \text{м} $
$ h_1 = 0{,}38 \ \text{м} $
$ m = 100 \ \text{кг} $
$ \rho_{\text{ж}} = 1000 \ \text{кг/м}^3 $
$ \rho_{\text{л}} = 900 \ \text{кг/м}^3 $

$ Найти: \quad S = ? $

$ Решение: $
Обозначим объёмы: \[ V_{\text{л}} = S \cdot h, \quad V_{\text{ж}} = S \cdot h_1 \] Применим закон Архимеда: \[ F_a = (\rho_{\text{л}} V_{\text{л}} + m)g = \rho_{\text{ж}} V_{\text{ж}} g \] Сократим $ g $ (g — сокращается): \[ \rho_{\text{л}} S h + m = \rho_{\text{ж}} S h_1 \] Выразим $ S $: \[ m = S(\rho_{\text{ж}} h_1 - \rho_{\text{л}} h) \] \[ S = \frac{m}{\rho_{\text{ж}} h_1 - \rho_{\text{л}} h} = \frac{100}{1000 \cdot 0{,}38 - 900 \cdot 0{,}4} = \frac{100}{380 - 360} = \frac{100}{20} = 5 \ \text{м}^2 \] $ Ответ: \quad S = 5 \ \text{м}^2 $

2.Какая часть тела окажется погруженной в жидкость, если плотность тела в n раз меньше плотности жидкости?

$ Дано: $
$ \rho_{\text{т}} = \frac{1}{n} \rho_{\text{ж}} $

$ Найти: \quad \frac{V_{\text{п}}}{V} = ? $

$ Решение: $
Если плотность тела в $ n $ раз меньше плотности жидкости, то для равновесия: \[ F_a = P \] Архимедова сила: \[ F_a = \rho_{\text{ж}} \cdot g \cdot V_{\text{п}} \] Сила тяжести тела: \[ P = \rho_{\text{т}} \cdot g \cdot V \] Приравниваем: \[ \rho_{\text{ж}} \cdot V_{\text{п}} = \rho_{\text{т}} \cdot V \] Подставим $ \rho_{\text{т}} = \frac{1}{n} \rho_{\text{ж}} $: \[ \rho_{\text{ж}} \cdot V_{\text{п}} = \frac{1}{n} \rho_{\text{ж}} \cdot V \] Сокращаем $ \rho_{\text{ж}} $: \[ V_{\text{п}} = \frac{V}{n} \] \[ \frac{V_{\text{п}}}{V} = \frac{1}{n} \] Это означает, что тело погружается в жидкость на $ \frac{1}{n} $ своей части.
$ {Ответ: \quad \frac{V_{\text{п}}}{V} = \frac{1}{n}} $