Момент инерции абсолютно твердого тела

Основные термины:

• инерция
• абсолютно твердое тело
• момент инерции

Инерция — свойство тела сохранять состояние покоя или равномерного прямолинейного движения, если на него не действуют внешние силы или их действие скомпенсировано.
Абсолютно твердое тело — модель, в которой расстояния между любыми точками тела остаются неизменными при любых внешних воздействиях.

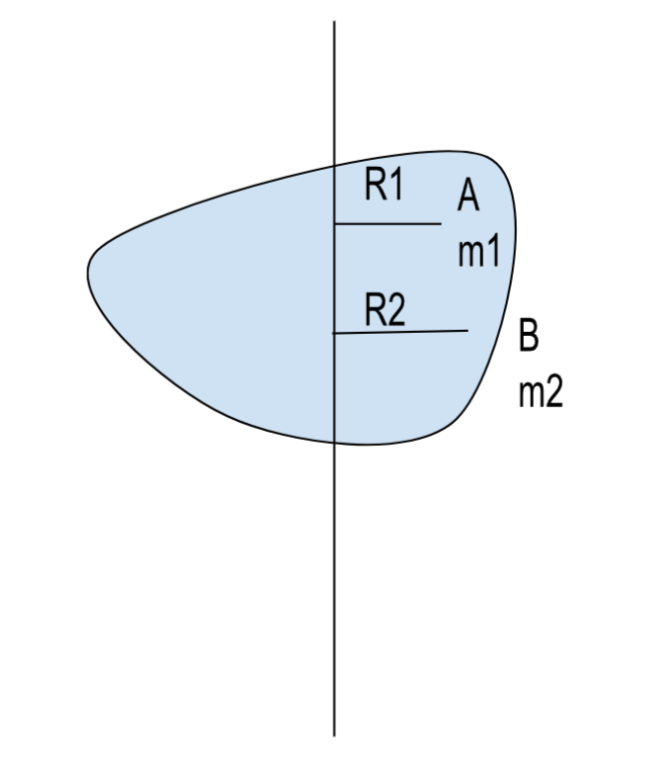
Момент инерции — физическая величина, характеризующая распределение массы тела относительно оси вращения. Определяет сопротивление тела угловому ускорению. Формула для материальной точки:
$$ J = mR^2 $$ где
\( m \) — масса точки,
\( R \) — расстояние от точки до оси вращения.

Угловая скорость — величина, характеризующая скорость вращения тела. Одинакова для всех точек тела, вращающегося вокруг одной оси.
Кинетическая энергия вращения (\( E_k \)) - энергия, связанная с вращательным движением тела. Вычисляется по формуле:
$$ E_k = \frac{1}{2} J \omega^2 $$ где \( J \) — момент инерции,
\( \omega \) — угловая скорость.

Рассмотрим тонкий зажимной радиус относительно осей вращения имело различную линейную скорость => создается различная кинетическая энергия => создается различная угловая скорость. Кинетическая энергия вращения (\( E_k \)): \( E_k = \frac{m v^2}{2} \quad \Rightarrow \quad E_{к.и} = \frac{m_i v_i^2}{2} ; \quad v_i = \omega R \quad \Rightarrow \quad E_{к.и} = \frac{m_i (\omega R)^2}{2} \quad \Rightarrow \quad \Sigma E_{к.вр.} = \Sigma E_{к.вр.} \quad \Rightarrow \quad \frac{\omega^2}{2} \Sigma (m_i R_i^2) \)

Теорема Штейнера
Позволяет найти момент инерции относительно произвольной оси, параллельной центральной: \( J = J_0 + m d^2 \) где \( J_0 \) — момент инерции относительно центральной оси,
\( m \) — масса тела,
\( d \) — расстояние между осями.

Ось вращения - линия, вокруг которой происходит вращение тела. Момент инерции зависит от выбора оси вращения.

Примеры решения задач

1. Определите момент инерции однородного диска радиусом 20 см и массой 1 кг относительно оси, перпендикулярной плоскости диска и проходящей через: а) центр диска и б) середину одного из радиусов диска.

\( Дано: \) \( R = 0.2 \ \text{м} \) \( m = 1 \ \text{кг} \) \( d = 0.1 \ \text{м} \) \( Найти: J_1, J_2 = ? \)

\( Решение: \) а) Для оси, проходящей через центр диска, момент инерции вычисляется по формуле: \[ J_1 = \frac{1}{2} m R^2 \] Подставим значения: $$ J_1 = \frac{1}{2} \cdot 1 \cdot (0.2)^2 = 0.02 \ \text{кг·м}^2 $$ б) Для оси, проходящей через середину радиуса, используем теорему Штейнера: \[ J_2 = J_1 + m d^2 \] где \( d = \frac{R}{2} = 0.1 \ \text{м} \). Подставим: $$ J_2 = 0.02 + 1 \cdot (0.1)^2 = 0.02 + 0.01 = 0.03 \ \text{кг·м}^2 $$ \( Ответ: J_1 = 0.02 \ \text{кг·м}^2, \ J_2 = 0.03 \ \text{кг·м}^2 \)

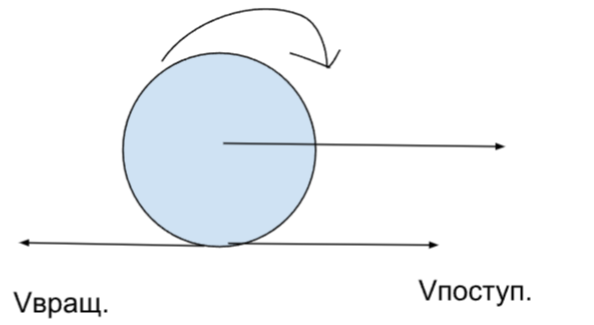
2. Шар массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Определите его кинетическую энергию.

\( Дано: \) \( m = 2 \ \text{кг} \) \( v = 4 \ \text{м/с} \) \( Найти: E_k = ? \)

\( Решение: \) Полная кинетическая энергия шара состоит из поступательной и вращательной энергии: \[ E_k = \frac{1}{2} m v^2 + \frac{1}{2} J \omega^2 \] Момент инерции шара: \( J = \frac{2}{5} m R^2 \). Для качения без скольжения: \( \omega = \frac{v}{R} \). Тогда: \[ \frac{1}{2} J \omega^2 = \frac{1}{2} \cdot \frac{2}{5} m R^2 \cdot \left(\frac{v}{R}\right)^2 = \frac{1}{5} m v^2 \] Полная энергия: \[ E_k = \frac{1}{2} m v^2 + \frac{1}{5} m v^2 = \frac{7}{10} m v^2 \] Подставим значения: $$ E_k = \frac{7}{10} \cdot 2 \cdot (4)^2 = \frac{7}{10} \cdot 2 \cdot 16 = 22.4 \ \text{Дж} $$ \( Ответ: E_k = 22.4 \ \text{Дж} \)