Деформация. Сила упругости. Закон Гука

Основные термины:

• деформация
• сила упругости
• закон Гука
• коэффициент жёсткости
• упругость
• модуль Юнга

Деформация — изменение формы или размеров тела под воздействием внешних сил.
Упругость — свойство материала возвращаться к своей исходной форме и размерам после удаления внешних сил и деформаций.
Типы деформаций по упругости:

1. Упругая деформация — временное изменение формы или размера тела. После удаления силы тело возвращается к исходной форме.
   Происходит в пределах упругости материала.
2. Пластическая деформация — необратимое изменение формы или размера тела. Материал остаётся деформированным после удаления силы.
   Возникает при превышении предела упругости.

Типы деформаций твёрдых тел:

• Сдвиговая (тангенциальная) деформация — изменение формы при сдвиге слоёв материала без изменения объёма.
• Растяжение — удлинение материала под действием силы.
• Сжатие — сокращение материала под действием силы.
• Изгиб — искривление материала под действием силы.

Закон Гука - закон, утверждающий, что деформация материала пропорциональна приложенной силе, при условии, что материал остается упругим и не превышает предел упругости.
Сила упругости- сила, возникающая в теле в ответ на деформацию и стремящаяся вернуть тело в его исходное состояние.

$$F_{\text{упр}} = k \cdot \Delta x $$ где
\( F_{\text{упр}} \) — сила упругости (\(Н\)),
\( k \) — коэффициент жёсткости (\(Н/м\)),
\( \Delta x \) — удлинение: \(\Delta x = x_2 - x_1 \) (в метрах)

Коэффициент жёсткости — сила, необходимая для изменения длины пружины на единицу: $$ \quad k = \frac{\sigma}{\varepsilon}$$
где \( \sigma \) — напряжение,
\( \varepsilon \) — относительная деформация.

Напряжение - это физическая величина, которая выражает внутренние силы, которые соседние частицы в непрерывной среде оказывают друг на друга $$\quad \sigma = \frac{F}{S}$$
где \( F \) — сила,
\( S \) — площадь поперечного сечения.

Деформация \((ε)\)-это относительное изменение размеров или формы материала под воздействием напряжения. Формально, деформация определяется как отношение изменения длины. $$\varepsilon = \frac{\Delta l}{l}$$

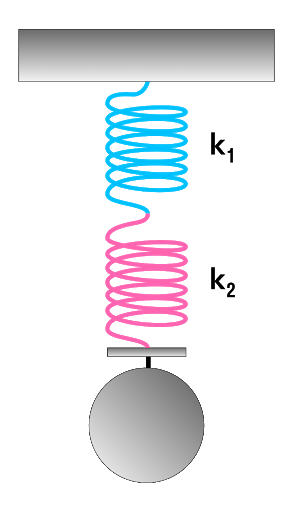
Параллельное и последовательное соединение пружин

	Последовательное соединение характеризуется одной точкой соединения пружин. Жёсткость системы находится по формуле $$ \frac{1}{k} = \frac{1}{k_1} + \frac{1}{k_2}$$
	При параллельном соединении пружины параллельны, т. е. их концы не связаны с друг другом, а жесткости складываются $$ k = k_1 + k_2$$

Модуль Юнга- общее название нескольких физических величин, характеризующих способность твердого тела (материала, вещества) упруго деформироваться (принимать в итоге первоначальный вид после приложения силы) при приложении к нему силы. $$E = \frac{\sigma}{\varepsilon}$$

Примеры решения задач

1.Дана пружина длиной 8 см, к ней приложили силу, в конечной точке растяжения которая была равна 320Н. Какой стала длина пружины если ее жесткость равна 800 н/м?

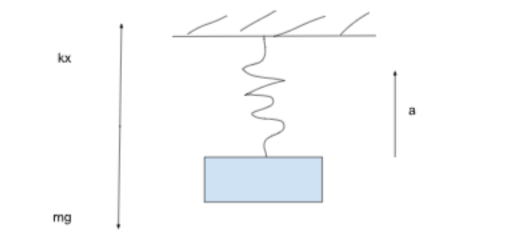
2.Пружину, на которую подвесили груз массой 0,4 кг, за свободный конец поднимают вертикально вверх с ускорением 0,8 м/с2. Жесткость пружины 250 Н/м. Пренебрегая массой пружины, определите на сколько увеличилась её длина по сравнению с недеформированным состоянием. Какую скорость приобретет этот груз через 5 с от начала движения?

\( Дано: \) \( m = 0{,}4 \ \text{кг} \) \( a = 0{,}8 \ \text{м/с}^2 \) \( k = 250 \ \text{Н/м} \) \( t = 5 \ \text{с} \) \( Найти: \ x = ? \), \( v = ? \)

\( Решение: \) \[ ma = F_{\text{рез}} = F_{\text{упр}} + mg \] Ось \( OY \): \[ ma = F_{\text{упр}} - mg \] \[ ma = kx - mg \] \[ x = \frac{ma + mg}{k} \] \[ x = \frac{m(a + g)}{k} = \frac{0{,}4 \cdot 10{,}8}{250} = 0{,}017 \ \text{м} \] \[ v = v_0 + at = 0{,}8 \cdot 5 = 4 \ \text{м/с} \] \( Ответ: \quad x = 0{,}017 \ \text{м}, \quad v = 4 \ \text{м/с} \)

3.Рассмотрим стальной проволочный стержень длиной 2 метра и площадью поперечного сечения 0,001 м². Если на стержень действует сила растяжения 10 кН, определите:

1)Напряжение в стержне

2)Деформацию стержня.

3)Модуль Юнга для стали равен 2×1011 Па. Определите изменение длины стержня.